Inertial Navigation System

Simulations of aerospace vehicles most likely require a model of an inertial navigation system (INS). I cannot imagine a modern missile or aircraft that does not employ an INS for navigation. There are the ballistic missiles with their high- precision gimbaled platforms, the passenger planes with laser gyros, and tactical missiles with inexpensive strap-down systems.

If you are tasked to simulate an INS, you can approach it from two aspects. Either you duplicate mathematically the functioning hardware with its imperfections, or you use the analytical error equations to corrupt the true navigation states. The first approach is used for detailed INS studies, whereas the analytical method is better suited for system-level performance studies. Our focus is on system simulations where I concentrate on the error equation approach and leave the more difficult task of hardware simulations to the experts.

Sir Isaac Newton unknowingly laid the foundation for inertial navigation. His second law states that position can be determined by integrating the vehicle’s acceleration twice. The acceleration is measured by an accelerometer. If the vehicle flew perfectly level, all we would have to add is a computer to carry out the integrations. However, missiles pursue targets, aircraft climb and descend, and satellites gyrate. To level the accelerometers, either they are mounted on a gimbaled platform, or a computer keeps track of the rotation between the accelerometers and inertial frames. For distinction, they are called either platform or strap-down INS.

The leveling of accelerometers requires gyroscopes. Their signals are used to ei­ther torque the platform or to determine the transformation matrix computationally. In both cases the so-called transfer alignment process will initialize them.

My treatment of INS simulations will be brief, with emphasis on error models that stood the test of performance studies. I assume that you have some familiarity with INS or are willing to acquire it by reading any of the standard reference texts. Two classics stand out, the book by Britting17 and a report by Widnall and Grundy.18 Britting treats a variety of INS systems from space stabilized to local-level platforms and strap-down systems. He painstakingly shows that the error equations of all of these various mechanizations can be condensed into one analytical form. More recent texts include detailed accounts by Chatfield19 and a broader treatment by Biezad.20

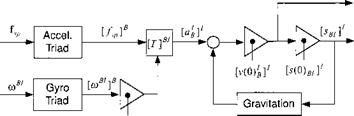
The fundamental equations of INS navigation, based on Newton’s law, calculate the velocity of the vehicle c. m. wrt the inertial frame in inertial coordinates [iJg]7 and its position wrt an inertial reference point /, [sg/]7 in inertial coordinates

d t

with [ /sp]B the specific force measured by the accelerometers, and [g]7 the gravi­tational acceleration in inertial coordinates. The accelerometers could be mounted on the vehicle or on a platform. In either case ]B stands for the coordinate system

associated with that frame. The integration of the gyro’s angular velocity of the vehicle wrt the inertial frame, expressed in inertial coordinates [шш]1, delivers the rotation tensor of the body frame В wrt the inertial frame | RBr! = T]BI. Figure 10.24 depicts these operational equations in block diagram form. Starting with the acceleration alB]B and rate [coBI B measurements, the transformed specific force, combined with the gravitational acceleration, is integrated twice to attain the vehicle’s position track. Six differential equations have to be solved for the basic navigation solution. Another four quaternion differential equations calculate the attitude angles.

Because the focus is not on the actual hardware, but rather on the error contri­bution of the INS to vehicle performance, I concentrate on their error equations. Both, the inertial and local-level systems will be discussed, for space and atmo­spheric vehicles, respectively. My approach is to corrupt the true values by the INS errors, thus providing the computed navigation data to the rest of the sim­ulation. Figure 10.25 shows the process of modeling navigation parameters with uncertainties. The є indicates perturbations, and the caret reflects computed values.

Are you ready to plunge into the details? As you will see, I shall make use of the perturbation methodology of Chapter 7 and derive the error equations of the space-stabilized navigator. To attain the error equations of terrestrial navigators, I elevate the Earth to an inertial frame and introduce the leveling feedback. A state-based formulation will round out the discussions.