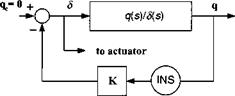
Rate damping loop

The most elementary autopilot function is the improvement of the dynamic stability of the vehicle, both in the pitch and yaw planes. This is accomplished by augmenting the aerodynamic damping derivative by rate feedback loops. The feedback sensors are the rate gyros from the INS system. We shall have to deal with the pitch and yaw planes separately. The pitch – rate autopilot is the same for both aircraft and missiles, although we may have to use different symbols, like lift slope Cia and the normal slope C^. The first one is given in velocity axes and the second one in body axes. Missiles prefer Сца, whereas aircraft use the more traditional Cia. If the missile has tetragonal symmetry, the yaw aerodynamics behaves like those of the pitch plane, and therefore the same autopilot serves both planes. In the aircraft case, however, the lateral aerodynamics is distinctly different and requires a separate treatment.

Let us apply the pole placement technique to this simple example. We employ the open-loop transfer function of the pitch plane, close the loop with a gain, and calculate the closed-loop poles. Because the gain is a free variable, we can choose it such that the closed-loop damping achieves a desired value for all flight conditions.

From Sec. 7.4.2 we carry over the linear perturbation equations of the missile pitch plane in the two state variables x = [q a], pitch rate and angle of attack. (Note that in this autopilot section we adopt the bolded vector convention of modern control.)

where Na = (qS/m)C^a, Ns = (qS/m)CNs, Ma = (qSd/l2)Cma, Mq = [qSd2/ (2/2 W)JC,„;/, Ms = (qSd/l2)Cms are the dimensional derivatives for the normal

Fig. 10.11 Rate feedback loop.

force N and the pitching moment M <5 is the pitch control surface deflection; and V the flight speed. These plant equations are in the general form of

x = Fx + gu

Now we build the transfer function of pitch rate q with respect to pitch control <5. Take the Laplace transformation of the plant equation and solve for x(s)

sx(s) = Fx(s) + gu(s)

(si – F)x(s) = gu(s)

x(s) = Ф (s)gu(s)

where Ф(5) = (si — F)~l is the resolvant matrix. The input u(s) is <5, whereas the output _y(5) could be either q or a. The vector h(s) = [10] will pick the output q from the general relationship

y(s) = h<b(s)gu(s)

Therefore, the desired transfer function is

Ф)=їіф( ) Ms[s +NJV -(Ma/MS)(NS/V)] S(s) {S)8 s2 + (Na/V – Mq)s – Ma – MqNa/V

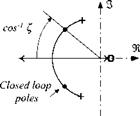You can verify this equation by comparing it with Roskam (Ref. 16, p. 426). The transfer function is positioned in a simple feedback loop (Fig. 10.11) and has two complex conjugate poles and a zero with the root locus pattern shown in Fig. 10.12. Selecting the closed-loop damping coefficient f determines the gain К.

To compute this relationship, we abbreviate the transfer function by

q(s) _ G(s + z)

S(s) s2 + as + b

and build the closed-loop transfer function

q(s) _ G(s + z) _ G(s + z)

q,(s) s2 + (a + KG)s + b + KGz, s2 + 2t;cons + со2

The last formulation introduces the desired closed-loop parameters £ and wn. Equating terms of equal powers in the denominator yields the formula for the rate loop gain

where the negative sign before the radical was discarded because it does not lead to a useful solution. The resulting natural frequency of the closed-loop poles, which follows from the selection of £, becomes

co„ — Vb + KGz

No matter what the flight conditions are, within the limitations of linear approx­imations the damping of the closed-loop response is guaranteed to be the value that you select. However, it could come at a penalty. A high gain K, causing a high natural frequency wn, may drive the controls prematurely into saturation. You need to check out the control deflections for some of the more extreme flight conditions before you commit to a desired f. If you cannot reconcile all conditions with one value £, you could make it dependent on dynamic pressure.

The calculation of A" in a simulation and in an actual flight control system is carried out on-line, making use of sensors and stored data. Tables provide the aerodynamic data and mass properties, while Mach number and dynamic pressure come from the air data computer. Combined, they establish the transfer function parameters. Together with the required damping f, the gain К can be computed.

This simple rate loop is used in the CADAC SRAAM6 simulation, Module C2, Subroutine C2RATE. It works quite well during the initial phase, as the missile leaves the launch rail, requiring stabilization. Because the SRAAM6 has tetragonal symmetry, both pitch and yaw channels have identical rate loops.

The GHAME6 simulation of the hypersonic SSTO vehicle requires a yaw sta­bility augmentation system (SAS). Our rate loop satisfies this need, yet must be adjusted to airplane yawing conventions. A positive /3 generates a negative side force Y, whereas a positive a causes a positive normal force N. Accounting for this difference, the linearized perturbation equations in the yaw plane are for airplanes

Г		LNr LNe	Ґ		~LNS~
A		1 1 AA I___	A	+	1 1___

where Yp = (qS/m)CYl,,Ys = (qS/m)CYi, LNp = (qSb/hi)Cnil, LNr = [qSb2/ (2/33 V)]C„,, LNj = (qSb//зз)СЛі are the dimensioned derivatives for the side

force Y and the yawing moment LN <5 is the rudder deflection. According to the pole placement procedure, we obtain the open-loop transfer function, again confirmed by Ref. 16, p. 458:

Ф) = LNs[s — Yp/V + (LNp/LNs)(Ys/V)]

<5(s) s2-(Yp/V + LNr)s + LNp + LNrYp/V ( ‘

and with the abbreviated closed-loop transfer function

rjs) _ ________ Gjs + z)_______ _ GQ + z)

rc(s) s2 + (a + KG)s + b + KGz s2 + 2£ cons + w2

We can use Eq. (10.72) again to calculate the yaw loop gain K. You can find an example for a yaw loop autopilot in the code CADAC GHAME6, Module C2, Subroutine C2YSAS.