A Lifting System with a Jet Flap in the Extreme Ground Effect

From the viewpoint of use in the transitional modes of motion (takeoff and touchdown) the so-called jet flaps have a certain practical interest. These flaps are formed by high-speed jets, utilizing the reserve of the air exhaust of turbojet engines blown through narrow slots of the trailing edges of the lifting system. Whereas the increment of lift due to the deflection of rigid flap is always accompanied by a certain increase of drag, jet flaps do not have this deficiency because the major part of the jet momentum gives rise to the thrust. Consequently, jet flaps favorably combine propulsive and lifting properties. One should also point out another reason that justifies the use of jet flaps. When the vehicle is operating in transient modes above rough seas, rigid flaps can touch the sea surface, thereby experiencing considerable hy­drodynamic loads. The latter circumstance can lead to failures in operation of the flaps and the corresponding flap control systems. The use of nonrigid devices, based on jet blowing, gives the possibility of controlling the lifting properties of the lifting system, including the cases when the jets touch the water surface. Assuming that the relative ground clearance is small the prob­lem of determining the aerodynamic characteristics of a wing with a jet flap can be effectively solved by the method of matched asymptotic expansions.

We start with the formulation of a nonlinear flow problem for a jet-flapped wing in the ground effect.

We consider a wing in steady motion with a jet flap along the trailing edge; see Fig. 6.8a.

In what follows, it is assumed that the jet is vanishingly thin. The latter assumption was introduced for the first time by Spence [143], who studied the two-dimensional problem for the flow past a foil with a jet flap in an unbounded fluid. No account was taken in Spence [143] of the ejection effect of the jet upon the surrounding fluid. However, both the results of Spence and other works, see, for example, Maskell and Spence [144], utilizing the

FLOW SUBDIVISION NEAR THE JET FLAP

b.

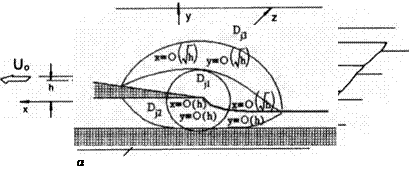
Fig. 6.8. Scheme of the flow past a wing with a jet flap in the ground effect: (a) general view; (b) near the jet flap.

hypothesis of the thinness of the jet, are in fair agreement with the experi­mental data even for large deflection angles up to 60°. These considerations justify the validity of the adopted mathematical model of a thin jet, in which expansion of the jet due to involvement into the motion of particles of the surrounding fluid is neglected.

The velocity potential of the flow past a wing with a jet flap should satisfy the Laplace equation, the flow tangency conditions on the wing and the jet sheet, the condition of the decay of perturbations at infinity, and the dynamic condition upon the jet surface. The Kutta-Zhukovsky condition at the trailing edge should be replaced with the requirement that the jet is blown at a given angle to the chord of the wing.

As in the general algorithm of the solution of the flow problem discussed in section 2, the flow field is conditionally subdivided into characteristic regions: the channel flow V under the wing and the jet sheet; the upper flow, including the region Vu above the wing; the jet sheet and part of the ground outside of the “shadow” of the wing and the jet on the ground; the regions of local flows near the leading and side edges Ve; and the local flow region in the vicinity of the trailing edge with a jet flap Dj. Below, based on the assumption of
the smallness of the relative ground clearance h <C 1, the main stages of the asymptotic solution of a steady flow problem for a wing with a jet flap will be shown. In accordance with the general hypothesis, the deflections of the jet sheet from the plane у = h are assumed to be comparable to the ground clearance, that is,

h-y} = 0(h). (6.38)

As indicated in section 2, such an assumption enables us to account for non­linear effects, at least in channel flow, with an asymptotic error of О(h2).

Special consideration is required of the local flow near the trailing edge with a jet flap. As for the rest, the solution procedure does not differ signifi­cantly from the approach discussed in section 2 for a wing without a jet flap. Therefore, corresponding modifications of the velocity potentials in regions Di, Vu, and Ve will be discussed very briefly.

At first, consideration is restricted to a vanishingly thin flat wing with a straight trailing edge moving at zero incidence. The full problem for the perturbed velocity potential <p is described by the Laplace equation

dx-2 dy2 dz2 ’

and the following boundary conditions:

• Flow tangency conditions on the wing, ground plane and the jet sheet:

• Dynamic condition on the jet:

Interacting with the oncoming stream, the jet experiences deformations. As a consequence, centrifugal forces occur proportional to the local lon­gitudinal curvature. These forces are balanced by the pressure difference across the jet surface

p – p+=/CC’/x, (x, z)eSj, x < 0, (6.43)

where the pressure can be calculated by the formula

(*>*)/

JC is the curvature defined though the coordinates y} of the jet surface as

C^C^(z) = 2l(z)/pU^l is the sectional coefficient of the jet momentum, 1(2) is the sectional jet momentum, plus and minus correspond to the upper and lower surfaces of the jet sheet, and Sj is the area of the jet sheet. The total jet momentum coefficient can be calculated by the formula

(6.45)

square of the root chord.

Rewriting the dynamic condition (6.43) taking into account (6.44) with asymptotic error 0(/i2), we obtain

direction within a distance of the order of 0(y/h)[29] Farther on, the jet sheet

In what follows, it will be shown, that for small relative ground clearances h, the main modification of the jet surface takes place in the downstream

loses longitudinal curvature, the pressure difference across it vanishes, and (in the case of a finite aspect ratio of the wing) generation of a vortex sheet begins. It can be easily seen that the dynamic and kinematic conditions work automatically in the case of a vortex sheet.

• The requirement of a jet blowing at a given angle r with respect to the chord of the wing:

As noted before in the problem under consideration, the Kutta-Zhukovsky condition at the trailing edge is replaced by the requirement that the jet should be blown at a given angle r = r(z) with respect to the chord at cross section z = const., i. e.,

душ

arctan —^ = r(z). for x = 0,

ox

where Xj is a local x coordinate, directed upstream.

• The condition of the decay of perturbations at infinity:

V(p —> 0, x2 + y2 + z2 —> 00.

Now, we turn to the asymptotic solution of the local problem of flow near a trailing edge with a jet flap. Consider a local flow in close proximity to a trailing edge equipped with a jet flap. Introduce local coordi­nates stretched in vertical and longitudinal directions, i. e.,

‘j а^( 0,г)]’ Vi a2{h*(0,Z)]

where /i*(0,z) is the local distance of a point on the trailing edge from the ground at a given cross section z = const., in our case of a wing of zero lateral curvature one can set h*(0, z) = h.

The stretching functions o and cr2 are to be determined by the least degeneracy principle. Note that, depending on the choice of the stretching functions and the lowest order asymptotics of the local flow potential in the region Dj, it is possible to distinguish different local subdomains for which the local flow descriptions would have corresponding distinct limiting forms. The subdivision of the jet flow domain Vj into different subdomains, as well as respective orders of coordinates, are shown in Fig. 6.8.

In the subdomain V^, independent variables are of the order Xj = 0(h) and 2/j = 0(h), so that one can set o(h) = h and 02(h) = h. Substitution of stretched variables in the full flow problem leads to the local flow problem in the immediate vicinity of the hinge of the jet flap. The solution of the latter problem was obtained in the following form:

• On the upper surface of the wing-jet,

g£ = _^in%+K+ (6’48)

• On the upper surface of the wing-jet,

= ~~ ln[l ~ ехрСтпг,,] + K7, (6.49)

where <p-}1 is the flow velocity potential in subdomain 2?^, — x^/h, 7£r,

and Tfcjj are unknown parameters to be determined by matching.

It follows from expressions (6.48) and (6.49) that the flow velocity near the point of blowing has a logarithmic singularity with different signs on the upper (acceleration) and lower (deccelaration) surfaces of the wing-jet. In subdomain X>j1? the jet degenerates into a segment of a straight line, so that the kinematic boundary condition coincides with the requirement that the jet is blown at a certain angle. The solution obtained in is two-dimensional and describes the local flow at distances of the order of 0(h) from the hinge of the jet flap. The most complete description of the jet can be obtained in subdomain V]2. Under the wing and jet c Pj2, it is convenient to choose the stretching function in the vertical direction as 02(h) = h. Longitudinal stretching о і (h) should be selected so that the mathematical description of the jet is the least degenerate. It means that to the lowest order, one has to retain both the dynamic and kinematic boundary conditions on the jet. We analyze in more detail the procedure of constructing the solution in subdomain V]2. To retain the channel flow for h —> 0, it is logical to assume later on that for h -> 0

o2 = h<£o1(h). (6.50)

Equation (6.50) implies that in the limit /1 0, we will obtain a one­

dimensional description of the flow under the wing and jet in the vicinity
of the flap. In this case, the dynamic boundary condition on the jet acquires the form

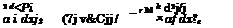(6.51)

The governing Laplace equation, it can be shown as previously, reduces to

The distinct limit for the system (6.51) and (6.52) is secured by the following choice of the stretching function (J{h) and the lowest order asymptotics of the local flow potential:

~ Gi(h)(p-} and <Ji(h) = y/h. (6.53)

With this in mind, equations (6.51) and (6.52) can be rewritten as

To obtain an equation describing the configuration of the jet sheet, we first integrate (6.55). We determine the constant of integration by requiring that at downstream infinity (x^ —> — oo), the jet becomes horizontal at any given cross section z = const. Therewith f/j -» y-}oo(z), and the perturbation ve­locity in the channel flow between the jet and the ground vanishes, i. e., for

where y-}oo(z) has to be determined by matching. Therefore,

Using (6.57) to exclude d(f-Jdx-n from (6.55), we derive the following differ­ential equation for determining the jet configuration:

C. wgf = 1 – fr – («8)

Multiplying both parts of (6.58) by yj, we can rewrite this equation as

Consistent with the previous requirement that for щ = щ{Щі) for any given z = const, the jet becomes horizontal, its slope must vanish too, i. e., for

X -» —00

Щ

dx^

Hence, we can determine the constant

C* = –

Thus, the differential equation governing the form of the jet becomes

It is not difficult to integrate (6.63) to obtain the following implicit equation for yj = Уі(хк):

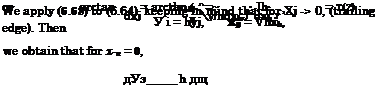Now, we can apply the requirement that the air should be blown from the trailing edge at a prescribed angle r = r(,z). Using (6.46) and accounting for the order of magnitude of the jet coordinates, that is,

Ф)

Vh,

and the distance of the jet from the ground far downstream is

Уіос (z) = 1 – Ф) Ш (6-70)

Setting y-}oo = 0 in (6.70), we can determine for which combination of sectional magnitudes of the parameters CM, r, and h the jet would touch the ground at a given cross section z = const.:

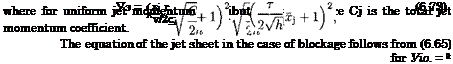For a uniform spanwise distribution of the jet deflection angle, the ground clearance and the jet momentum coefficient, equation (6.71) can be inter­preted as a condition of blockage, i. e., the situation when the jet touches the ground everywhere spanwise

and the blockage occurs at a distance

from the trailing edge.

The longitudinal velocity in a narrow channel under the jet sheet is given by equation (6.57), where y-]oo is described by (6.70). The spanwise distri­bution of the longitudinal perturbation velocity at the trailing edge can be obtained by setting Xj = 0,yj = 1, wherefrom

Due to the conservation of mass, the magnitude of dip-Jdx^ is practically the same as the perturbation velocity under the wing in the vicinity of the trailing edge. Therefore, to the lowest order, the boundary condition for the

channel flow equation at a trailing edge equipped with a jet flap can be written identically as

a-t(o’z)=T{z)fW – (6’76>

This can also be shown through the matching process.

The flow potential in the upper part of subdomain V]2 (x$2) was found in the form _

Vh = hvt + Лл/л(г/^- + V? ih) +0(h2), (6.77)

where (p+ and cpf (xj2) are unknown functions to be determined by matching. The next characteristic subdomain of the flow near the jet flap is Dj3, which is located above the wing and jet; see Fig. 6.8. In this subdomain, y} = О(Vh) and Xj = О(y/h). The expression for the flow potential in 2?j3 was found in the form

^ J 9i(0 Ц(Чз – О2 + У*,] d£+ • • •. (6-78)

where g(h) is an unknown gauge function of h, q(£) is an unknown function, and xj3 = xj2 = X) jyjh. Thus, as a result of the asymptotic analysis of

the flow field in near the point of jet blowing, we can determine the

characteristics of the flow in subdomains Dj1? Dj2, and V]3 with the help of expressions (6.57), (6.77), and (6.78). The unknown parameters and functions are determined by matching.

Continuing the discussion of particular features of the asymptotic algorithm for a wing with a jet flap in the ground effect, some cor­rections will be shown briefly, which have to be introduced into a general algorithm of the solution in the particular case of a wing with a jet flap. In the upper flow region Du, the expression for the potential (pu (2.31) has to be supplemented by the term

~ [ – cU, r = ^(x-02 + y2 + (Z – 02, (6-79)

47Г J2 r

which represents the potential of the distribution of sinks with strength along the trailing edge І2 and models the influence of the jet flap upon the upper flow. In subregion Ve near the leading edge and side edges, the velocity potential is given by expression (2.39), in which the coefficients a* depend on characteristics of blowing. If the wing has endplates, their influence upon the aerodynamics of the lifting system can be determined in the same fashion as for a wing without a jet flap.

In the channel flow V the equation for determining the potential (f has the same form as that for a wing without a jet flap. For zero pitch angle, the equation for the lower flow potential is
with boundary conditions at the leading edge and side edges to be determined by matching. Below, without going into details, some results are presented of the matching needed for further calculations. Matching the upper flow potential <pU) valid in region T>u, with solutions ip^ and ^ in subdomains Vi2 and Vj3 enables us to find the quantities g(h), j, and

where describes ordinates of the jet for large Xj2 —> —oo. Note that Уіоо depends on z, i. e., varies along the span, and Qj(z) is negative, i. e., represents the productivity of sinks, modelling local effects in the upper flow subdomain, connected with deformation of the jet surface from the trailing edge downstream.