Euler Transformation

Flight dynamics deals with many reference frames and their associated coordi­nate systems. Often the reference has to be changed, e. g., from Earth to inertial or body to local level. If the transformation involves time derivatives, tensor flight dynamics proceeds differently than vector mechanics. In vector mechanics the transformation is made at the coordinate level. For instance, Let A and В be two coordinate systems in which to express the time derivative of vector v, then

where u>BA is the angular velocity of В wrt A. This is not a tensor relationship, because the ordinary time derivatives give rise to the extra term on the right hand side.

Tensor flight dynamics employs a more general transformation, the so-called Euler transformation. By recognizing the distinction between reference frame and coordinate system and by introducing the rotational time derivative, the transfor­mation assumes tensor properties. With the arbitrary reference frames A and B, the rotational time derivatives of vector v wrt the two frames are related by

Da v = DB + flBAv

where 17s"4 is the skew-symmetric angular velocity tensor of frame В wrt A. An analytical proof will now be given of the Euler transformation, whereas the rational proof, based on the isotropy of space, can be found in Sec.4.2.4.

Proof: We introduce two arbitrary Cartesian coordinate systems, X;, X;, which

coordinate the arbitrary tensor of rank one D;, D,, and two coordinate systems, fixed

А В

in frames A and S, x, , x;, respectively, that coordinate the two special tensors of

A ^

rank one a,. b, , which have constant components in their respective coordinate systems. The coordinate transformations we will need are

A Vi = tjiVj	(D.71)
В = _
Vi = tjiVj	(D.72)
В BA A
Vi = tu Vj	(D.73)
pi	(D.74)

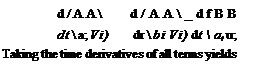The proof starts with two additive scalars, whose time derivative are equal in any coordinate system, and specifically in the A and В coordinates:

л d a A d a d а а в d в d в в B d в

at — Vi…………. + bi —vj+— bi Vi щ — Vi + —Щ vi + bi — vt

dr dr dr dr dr dr

A в

To find expressions for the two time derivatives dbt /dt and da; /dr we use the rotational time derivative, Eq. (D.22), recognizing the fact they are zero for their respective vectors

from which follows

d В BA d BA в

~T~ tti tjk “ Г//; d[

dt dt

and similarly

d A AB d AB A

~T~ bi = Uk ~Г~ Ьк bi

dr dr

Substituting both equations into Eq.( 4.8 ) yields

A AdA /В B d В AB d AB A A BA d BA В В

ai + bi J — Vi = la; + bi J — Uy + tik — tik bi Vi – tik — t, k Щ Vj (D.80)

Let’s convert the second term on the right-hand-side to В coordinates, by using the first transformation of Eq. (D.73) and use the fact that reversing the transformation from A wrt В to В wrt A is the same as taking the transpose:

AB BA

tij = tji (D.81)

Then we have for the second term on the right-hand-side of Eq. (D.80):

AB d AB A A BA d BA В B

Uk ~7~ tik bj Vj — tji ~7~ tnl bi vn (D.82)

dr dr

Now we want to reverse the sign of the last term of Eq. (D.80) by developing a relationship from the time derivative of the unit tensor,

which results in

We have obtained the desired sign change of the last term of Eq. (D.80) after relabeling of subscripts:

BA & BA в В BA d BA в В tik ~T~ tik tV = hi ~T~ hi I (Iі Vn d t d t

Substituting this equation and Eq. (D.81) into Eq. (D.80) provides us with the simplified relationship

Now, the left side is transformed to x, coordinates, as well as the first factor on the right-hand-side, whereas the second factor is transformed to the x-t coordinates:

-,d__ = . . / d,= = . BA d ba= _

t ji [&j H” bj) {t(i’ ^/) = t ki j ® j ) ( ^ }mi Vm ) H” Ul ^nl t pn^ p

(D.87)

After deleting the common factor (aj + bj) and expanding the time derivative, we obtain the main result:

d _ d _ _ / d _ = d = _ = BAdBA-

^ tt/ “I – ty/“ t//U/ — t^j I “ Vk T" t ki t oi W T" tki hi tni tpnVp j (D.88)

We recognize the rotational time derivatives on both sides of the equation and an extra term; all connected by the arbitrary transformation tkj:

Because the rotational time derivative is a tensor, the extra term must also be a tensor and, therefore, this equation is a tensorial relationship. Again, because vp is a tensor, it follows from the quotient theorem (Ref. 4, p. 90) of tensor calculus that

BA d BA
til ~7~ tnl
dt

is a tensor of rank two, transformed from the В to the two-barred coordinates. It is the angular velocity tensor of frame В wrt frame A, coordinated in the В system. In matrix notation we write it as [£2ВД]В.

Continuing in matrix notation, if we introduce for x-t —*■ ]" and x, —*■ ]", we converge on the relationship

[DAvf = IT]"" ([DBvf + [£2вд]"[и]") (D.90)

Because [T}M is the transpose of the transformation matrix between any two Cartesian coordinate systems, the equation can be written in the symbolic tensor

TThe overbar of T indicates the transposed of the matrix.

form,

Da = Db + ПВА (D.91)

and the Euler transformation has been proven by purely analytical means. The angular velocity tensor is skew-symmetric, which can be proven from the general theorem of tensor analysis that states the following: A skew-symmetric tensor is a tensor (of any rank) whose components change sign under any odd permutation of its indices. Starting with Eq. (D.84), exchanging the free indices on the right side establishes the proof. Because ilBA is skew-symmetric, it has the axial vector – equivalent utBA.

D.5 Conclusions

In this appendix the key elements of tensor flight dynamics have been given a sound analytical basis. In general space-time, an operator was identified that ac­counts for changing time. For the special Euclidean/Cartesian space this operator is called the rotational time derivative. It was shown that, when operating on ten­sors, it preserves their tensorial character even under time-dependent coordinate transformations. This is not true for the ordinary time derivative that is exclusively used in vector mechanics. In the latter only time-independent coordinate transfor­mations maintain invariance. In tensor flight dynamics the covariance principle is realized because of the recognition that reference frames and coordinate systems are distinctly different entities—physical vs mathematical. Newton’s law, being a law of physics, should therefore be referred to an inertial frame and not an inertial coordinate system. Changing reference frames is also a physical concept and is governed by the Euler transformation. Its tensor form was analytically derived from general principles.

Both, the rotational time derivative and the Euler transformation are the under­pinning of tensor flight dynamics. Though Gibbs’ vector mechanics has served us well, tensor flight dynamics’ focus on modeling the physics first, followed by coor­dination and matrix programming, has enabled the building of ever more complex computer simulations. It is hoped that the novelty of tensors will find widespread acceptance for the effectual formulation of flight dynamics.

References

‘Gibbs, J. W., The Scientific Papers of J. Willard Gibbs, Ph. D, LL. D., Volume 11, Dover, New York, 1961.

2 Adler, R., Bazin, M., Schiffer, M., Introduction to General Relativity, McGraw-Hill, New York, 1965.

3Wundheiler, A., “Kovariante Ableitung und die Cesaroschen Unbeweglichkeitsbedin – gungenf Mathematische Zeitschrift, Vol. 36, 1932, pp. 104-109.

4Lass, H., Elements of Pure and Applied Mathematics, McGraw-Hill, New York, 1956.

[1] Time and space are homogeneous. There exists no preferred instant of time or special location in space.

[2] is the abbreviation for d/dt | vB |, [TI1V is given by Eqs. (9.8) or (9.11), and [T JVL byEq. (9.21). The state variables of the linear differential equations are V, фуВ, вуВ. For the Hat-Earth case the second and third equations become singular if V cos 6VI or V are zero. Therefore, we cannot simulate a missile that takes off vertically, an aircraft that dives straight to the ground, or, for that matter, a hovering helicopter. Fudging the initial conditions can help us get started, and once underway we program around the singular values until the equations are again well behaved. The errors incurred may be tolerable, as experience has shown.

[3] Initialize the geodetic latitude with the geocentric value Xd = kc = arcsin

[(■5в/)з/І5В/|]-

[4] [A] — к[Я]| = 0