Nonlinear Steady Flow Problem for a Foil with a Jet Flap

Consider a jet-flapped foil with the upper and lower surfaces described by yu and y moving above the flat ground at incidence в. The jet deflection angle is designated r, and the jet momentum coefficient Cy In the simplest case of the extreme ground effect, that is to the lowest order, we have to solve a simple differential equation

Equation (6.85) has to be solved with the following trailing edge condition:

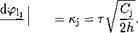(6.86)

Solution of the flow problem in an approximation of the extreme ground effect is straightforward. The lift coefficient was obtained in the form

СУі = l-(l-«j)2(l-Cyo), (6.87)

In the concrete case of a flat plate of infinite aspect ratio with a jet flap in the extreme ground effect, expression (6.88) yields

(l-*j)2 . (1 -ТуїЩЩ1

1+9 1+9

1 dx 1 »?(*)’

where 6 = 6/h and h is the relative ground clearance. The general algorithm of the flow problem solution enables us to proceed to higher approximations. Omitting intermediate calculations, one can present the following formulas for the lift coefficient of a moderately thick foil with a jet flap:3

– {Б2 – A2 + (0 + ^) (r^ + in

-(l-«j)[51-y1′(0)(l-«j) + y((0)(l-lnTr)] Ґ^-Л (6.93)

Jo У x))

(Vw ~ V2O1 + y/y~)

(Vvi + vIO1 – VS5D ’

For «j = 0, these formulas for Cy yield corresponding formulas for the foil without a jet flap, obtained in paragraph 4.1. In the case of a jet-flapped flat plate in the extreme ground effect, when yu = y = 1 + Qx,

That is, with thickness of the order of the ground clearance.

– j)

.0 + rj + iT0(1-*j)

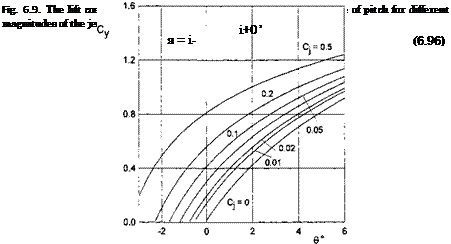Figure 6.9 presents the lift coefficient Cy of a flat plate versus the angle of pitch 9° for different magnitudes of the momentum coefficient Cj and the angle of blowing r° = 30° for h = 0.1.

1+* 7Г

Figure 6.10 shows the dependence of the lift coefficient of a jet-flapped plate upon the relative ground clearance for r° = 15°, 9° = 2° for different magnitudes of the jet momentum coefficient Cy Linearizing the expression for the lift coefficient Cy of the flat plate, we obtain the formula

where 7e = 0.5772 is Euler’s constant. This formula is identical to the ex­pression derived within assumptions of the linear theory in Kida and Miyai [50].