Aliasing
The fundamental wave number range of a finite difference scheme is – n < a Ax < n (see Figure 2.1). The a Ax versus a Ax curve in the range – n < a Ax < 0 is obtained by an antisymmetric extension of that in the range 0 < a Ax < n. Wave numbers that fall outside this range are underresolved. Their wavelength is less than two mesh spacings. They are aliased back inside the fundamental range. To determine the relationship between the original wave number and the aliased wave number, consider the initial condition (7.4). Let f(x) = Ф (x), where Ф is a Gaussian with a concentration of wave number around a0 ; i. e.,
![]() t = 0, Ф(x) = e-(ln2)(і)2+ia0x.
t = 0, Ф(x) = e-(ln2)(і)2+ia0x.
The Fourier transform of Eq. (7.28) is
If b, the half-width of the Gaussian, is large, then Eq. (7.29) confirms that there is an essential concentration of wave number around a = a0.
Let Ax be the mesh size used in a computation. l is the spatial index so that x = lAx. As far as the computation on the mesh is concerned, Eq. (7.28), in the discretized form, is
Ф1 = e-(ln2)(Tr)2+ ia0lAx. (7.30)
It will be assumed that a0Ax > n but less than 2n. Since a0Ax is larger than n, let
![]()
![]() a0Ax = n + 5.
a0Ax = n + 5.
But
eia0Axl = ef[2n + (5-n)]l = ei(5-n)l = ei(5-L)x = Є (a0 Ax )x Therefore, the initial condition is the same as
t = 0 Ф (x) = e-(ln2)( і )2+i(a0- Ax)x for the computation. In other words, the effective wave number is
Hence, although a0Ax is larger than n, it is aliased back into the fundamental range by a shift of 2n.
As an example, consider the function
![]()
 |
(7.35)
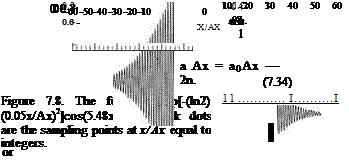
The wave number of this function concentrates around a0Ax = ±5.48. This is outside the fundamental range. For computation on the mesh, the effective wave number, according to Eq. (7.34), is aAx = ±0.803. Figure 7.8 shows the original function (7.35), with wave number concentrates around a0Ax = ±5.48. The black dots in the figure are sampling points. From the finite difference computation point of view, only the sampling points matter. Figure 7.9 shows the function representing the sampling points. This function is the same as
This function has a low wave number of aAx = ±0.803 and lies inside the fundamental range of wave numbers.













