Coefficients of Several Large Damping Stencils

When large computational stencils are used for increased spatial resolution, it is a good practice to use large artificial selective damping stencils as well. The coefficients of several large damping stencils are provided below.

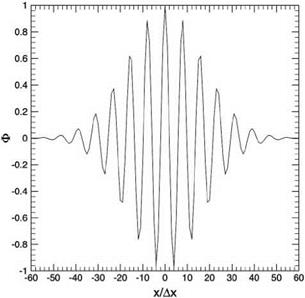
Figure 7.9. The aliased function of Fig­ure 7.8.

9-Point Stencil

a = 0.1975п, в = 1.28 d0 = 0.24771185403726 d4 = d_! = -0.20711771710355 d2 = d_2 = 0.11853742369381 d3 = d_3 = -0.04288228289644 d4 = d_4 = 7.606649287550E-3.

11-Point Stencil

a = 0.195п, в = 1.45 d0 = 0.22311349696678 d4 = d_4 = -0.19226925045875 d2 = d_2 = 0.12201457655441 d3 = d_3 = _0.05522898418946 d4 = d_4 = 0.01642867496219 d5 = d_5 = _2.5017653517767E-3.

13-Point Stencil

a = 0.1925п, в = 1.63 d0 = 0.20975644405137 d4 = d_! = _0.18327489344470 d2 = d_2 = 0.12192070829492

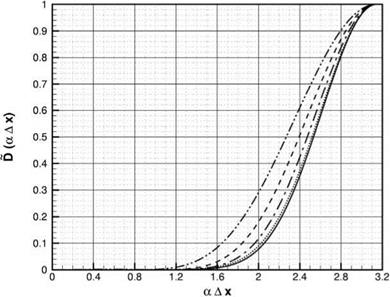
Figure 7.10. Damping functions corresponding to several large damping stencils. – • • —, 7- point stencil;——- , 9-point stencil;——- , 11-point stencil;……….. , 13-point stencil;——– , 15-point stencil.

d3 = d-3 = -0.06111106887629 d4 = d-4 = 0.02244708528388 d5 = d-5 = -5.6140376790013E-3 d6 = d-6 = 7.539843954985E-4

A plot of these damping functions is given in Figure 7.10.

EXERCISES [6] [7] 2 [8]

d U d U d [9]U dt + C 9x V 9×2 ’ The exact damping function on the right side of the equation is D(aAx) = (a Ax)2.

d2u 9 v 9 u 9×2 9x’ V dx

(a) Discretize v(92u/9×2) directly using a second-order central difference scheme to yield

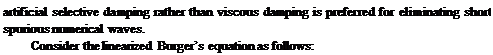Find the damping function in wave number space.

(c) Which approximation is more accurate in terms of reproducing the effect of physical viscosity over the resolved wave range?

(d) Which approximation would help to damp out spurious short waves?

(e) If the objective is to damp out spurious short waves alone with little damping on the long waves, is artificial selective damping better, or are physical viscous terms better?