Computation of Nonlinear Acoustic Waves

Figure 8.1. (a) The P, C+, and C— characteristics in the x — t plane. (b) Characteristics of equation (8.13) and nonlinear steepening of the wave front.

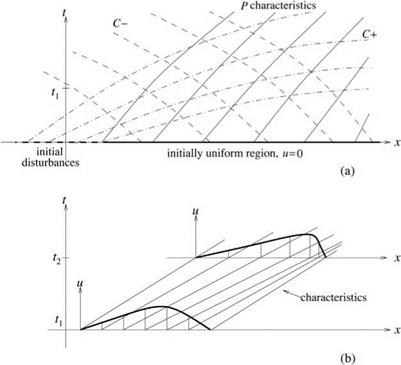
Now consider the problem of acoustic waves propagating into a region initially at rest; i. e., t = 0, u = 0, p = p0, a = a0. Without loss of generality, it will be assumed that the waves propagate in the positive x direction. Since this region is covered by the P characteristics that start out from the same initially undisturbed region (see Figure 8.1), the isentropic relation

dp dp 2 = a = da p a p y — 1
P_ pY	£0 P0
(8.8)
or

holds throughout the region. The same is true with the C characteristics. By elimi­nating dp/pa from Eqs. (8.7) and (8.8), it is found that

(8.9)

Upon integrating Eq. (8.9) and noting that the constant of integration is the same for all points in the region, the following integral relation is obtained:

2a 2a0

— u = – Y — 1 Y — 1

Now, in the region of the x — t plane covered by both the P and C— characteristics starting from the initially uniform region, Eq. (8.2) may be cast into the following form, by means of the relation (8.7) of the C characteristics:

+ (u + a) — 0.

9 x

Finally, by combining Eqs. (8.10) and (8.11), it is easy to derive the nonlinear simple wave equation as follows:

d u / Y + 1 Tt + ( “°+ ~u

A = 0. д X

(8.12)

Eq. (8.12) is a nonlinear first-order partial differential equation for u. The char­acteristic system of this equation is

dx y +1

—— = «0 +– ~— u

dt 0

du 0 dt

The two equations of (8.13) can be integrated easily. Suppose the initial con­dition is

t = 0, u = <h(x). (8.14)

The integral of the second equation of (8.13) satisfying the initial condition is

t = 0, x = s, u = Ф(5). (8.15)

This means that u is a constant along a characteristic. Because u is a constant along a characteristic, the right side of the first equation of (8.13) is a constant. The integral of this equation is

x = s + ^a0 +Y 2 1 Ф^)^ t. (8.16)

The solution of the nonlinear simple wave equation (8.12) and initial condition (8.14) may now be found by eliminating the parameter s from Eqs. (8.15) and (8.16). Eq. (8.16) indicates that the characteristics are straight lines in the x – t plane. The slopes of the characteristics, however, depend on Ф^). If Ф^) is not a constant, the slope of the characteristics will vary from characteristic to characteristic (see Figure 8.1b). Note that adjacent straight lines that are not parallel but convergent will eventually intersect each other. Therefore, over a sufficiently long period of time, the characteristics of Eq. (8.16) will overlap each other. When this happens, the solution will become multivalued. To render the solution single-valued, a discon­tinuity or a shock must be inserted into the solution. In this chapter, shock-capturing computation using the dispersion-relation-preserving (DRP) scheme is considered.

 

8.1 Nonlinear Simple Waves

 

One-dimensional acoustic waves are governed by the continuity, momentum (invis­cid), and energy equations. They can be written in the following form:

 

dp dp du dt dx H 9 x 9 u 9 u 1 9 p + u + — 0 dt dx p dx 9p 9p du — + u— + у p— — 0. dt dx dx

 

(8.1) (8.2) (8.3)

 

It is well-known that the above first-order system has three characteristics: the P, the C+, and the C characteristics (see Appendix C for derivation).

 

8.1.1 The P Characteristic Along the P characteristic

 

(8.4) (8.5)

 

8.1.2 The C+ and C – Characteristic Along these characteristics,

 

dx — u ± a, dt

 

(8.6)

 

where a — (yp/p)2 is the speed of sound, the dependent variables are related by

 

pa