Outflow Boundary Conditions: Further Consideration

In many CAA simulations, the boundary of the computation domain cuts across an outflow. An example is the case of simulating jet noise generation as shown in Figure 9.2. Since numerical boundary conditions imposed at the outflow boundary must reproduce all the external effects on the flow field inside the computational domain, the outflow boundary is usually placed sufficiently far downstream of the nozzle exit to avoid significant upstream influence of the jet flow left outside. In the jet noise simulation problem, as in many other problems, the mean flow is not known a priori. The numerical boundary conditions are required to capture the mean flow as well as to be transparent to the outgoing acoustic, vorticity, and entropy waves.

At present, many CAA boundary conditions are formulated under the assump­tion that the mean flow is known. Their main concern is to avoid any reflection of the outgoing unsteady disturbances. Dong (1997) recognized the need for CAA outflow boundary conditions to be capable of capturing the mean flow correctly as well. He proposed a set of asymptotic outflow boundary conditions based on sink/source flows. In two dimensions, these conditions are as follows:

1 dp dp 2

—– 77 + 7—— + – (p – px) = 0

ax dt 9 r r

1 9 и 9 и и

———– 1—— + – = 0

ax dt 9 r r

1 9 v 9 v v

———– 1—— + – = 0

ax dt 9r r

1 9 p 9 p 2/

—– 77 + 7—— + _ (p

ax dt 9r r

where r is the radial distance in polar coordinates, and px, px, and aX are the ambient pressure, density, and sound speed, respectively. Dong derived this set of outflow boundary conditions by noting that the asymptotic solution of a time – independent localized source in two dimensions, denoted by an overbar, is

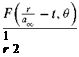where Q is the source strength, у is the ratio of specific heats, and vr is the radical velocity component. It is easy to verify that Eq. (9.7) is a solution of Eq. (9.6) to order O(r-4). On the other hand, the asymptotic solution of outgoing acoustic waves in two dimensions without mean flow (see Eq. (6.1)) is

By substitution of asymptotic solution (9.8) into Eq. (9.6), it is easy to find that Eq. (9.6) is satisfied to order O(r-3/2). It has been pointed out that Eq. (9.6) is very similar to the asymptotic boundary conditions of Chapter 6, Eq. (6.14). The major difference is in the numerical coefficients of the 1 /r terms. It is straightforward to see that the asymptotic solution of the mean flow of a localized source and that of the outgoing acoustic waves have different dependences on r. Eq. (9.6) as an outflow boundary condition is a reasonable compromise.

Outflow boundary condition (9.6) may be generalized to three dimensions. The corresponding equations in spherical polar coordinates (R, в, ф) are as follows:

1_ dp + дР + 3(P – ) = 0

дt дR R

1 дU дU 2u

— Ч7 + Т5 + – ІЇ = 0 aTO dt д R R

1 д V д V 2v

—– ~я7 + lyn + 17 = 0

a^ д t д R R

1 д W д W 2w

am д t д R R

1_ др + др + 3(p – )

aTO дt д R R

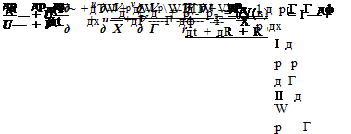Jet flows are not source flows. Boundary layer arguments as well as experi­mental measurements suggest that the static pressure across a jet far downstream is practically constant and is equal to the ambient pressure. In this case, p = pTO is a good mean flow pressure boundary condition. This is the steady-state solution of the jet outflow boundary condition. Now, if the outflow boundary conditions (6.13) are nonlinearized, i. e., replacing the linear convection term и0(дu/дх) by the full convection terms etc., it is easy to arrive at the following set of nonlinear outflow boundary conditions. Written in cylindrical coordinates (r, ф, x), they are

where V(e) = и cos в + a(1 – sin2e)1/2 and M = и/a; a = (yр/р)112 is the speed of sound; and (R, в, ф) are the spherical polar coordinates with the polar axis coinciding with the centerline of the jet. For the mean flow, р = рто is a solution for Eq. (9.10e). Eqs. (9.10b), (9.10c), and (9.10d) are identical to the momentum equations of the Euler equations. They should yield the correct velocity field. For a time-independent solution, Eq. (9.10a) reduces to

др др W др

и—— v——- ——– = 0.

дх дГ Г дф

Eq. (9.11) is the same as р = constant along a streamline. This should be rea­sonably good for jet flow far downstream where there is no intense mixing. Thus, outflow boundary conditions (Eq. (9.10)), although originally designed for outgoing disturbances alone, are also capable of capturing the mean flow of a jet.

Now, outflow boundary conditions (9.9) and (9.10) are very different. Each is designed specifically for a class of outflows. If the mean flow is source-like, then use Eq. (9.9). On the other hand, if the mean flow is jet-like, then Eq. (9.10) would be more appropriate.