The Aerodynamics of a Lifting System Near Curved Ground

7.1 The Influence of Waves on the Aerodynamics of a Lifting Surface

A large seagoing ground-effect vehicle has to combine sufficient seaworthiness with acceptable magnitude of the lift-to-drag ratio, when flying above rough seas. The approach of matched asymptotic expansions furnishes a simplified mathematical model of the unsteady aerodynamics of the wing-in-ground – effect vehicle, based on the idea of domination of the channel flow in the extreme ground effect. This concept seems to be promising for wave per­turbations, because the influence of waves upon the aerodynamics of such a vehicle is in fact predominantly due to the corresponding variation of the geometry of the gap between the wing and the sea surface.

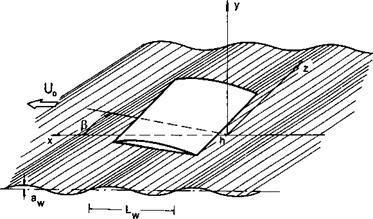
Following Rozhdestvensky [56, 57], we consider the schematized problem of a thin flat rectangular wing of aspect ratio Л, advancing with constant speed U0 and an angle of pitch в above a still, solid, wavy boundary.[31]

The wing and the coordinate system are presented in Fig. 7.1, where aw is the amplitude of the wave, Lw is the length of the wave, h is the clearance, measured from the trailing edge of the root section to the unperturbed level of ground surface, and (3 is the course angle measured in the horizontal plane у = 0 as the least angle between the direction of the wing’s motion and a normal to the front of a sinusoidal cylindrical wave.[32] As previously, one assumes that at any time the gap between the wing and the wavy ground is small compared to the chord. With these assumptions in mind, we can write the gap distribution between the wing and the underlying surface as

h*(x, t) = h + вх — aw cos[fc(£ cos(3 + z sin/? +1 cos/?)]

= hh*(x, t) = 1 + Ox — awcos(nx +pz + nt), (7.1)

Fig. 7.1. A lifting surface moving in proximity to the wavy ground.

where 9 9/h, aw — aw//i, к — k cos/3, p — fcsin/3, and к = 2tt/Lw is the

Strouhal number based on the ratio Lw of the wavelength to the root chord of the wing.

Using the lowest order model of the flow, we have to solve the problem described by relationships (2.114)—(2.117) with the gap distribution input given by (7.1). One of the approaches to the solution of this nonlinear problem for the motion of a wing over a wavy wall may be based on a consistent expansion of the velocity potential in terms of the two small parameters 9/h and aw/h; see Barrows and Widnall [136] and Rozhdestvensky [42]. In line with this approach, we seek the solution of the problem in the form of a series and leave only terms that are linear in the angle of pitch

V = 0<Po + 0<br<p§aw + • • •. (7.2)

Function <рё characterizes the linear (in angle of attack) part of the potential for steady motion above an unperturbed underlying surface. As shown in 3.4, the expression for can be readily derived for the uniform spanwise distribution of the angle of pitch in the form

2

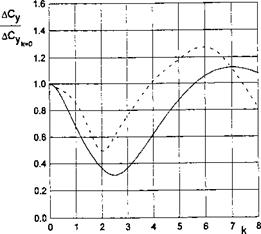
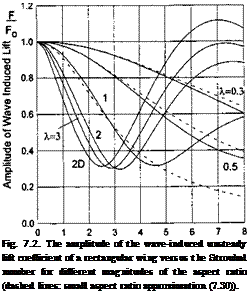
Figures 7.2 and 7.3 present the amplitude-phase characteristics of the wave – induced lift coefficient CVw (t) versus the relative wavelengths (Strouhal num­bers) for different aspect ratios of a rectangular flat wing. The dashed lines correspond to calculations performed by using the formulas (7.30) and (7.31) for wings of a small aspect ratio. It follows from Fig. 7.2 that at a certain relative wavelength for a wing of a given aspect ratio the amplitude of the wave induced unsteady lift is minimal. With a decrease in the aspect ratio, this minimum shifts toward the range of shorter waves. For example, for a wing of an infinite aspect ratio, the minimum amplitude of the unsteady lift is reached at к ~ 2.4, Lw ~ 2.6.

For a rectangular wing of aspect ratio A = 2, this minimum is reached at к ~ 3.1, Lw ~ 2,[33] and for a square wing Л = 1 the minimum occurs at

Strouhal Number i<= _2j_

L

L w

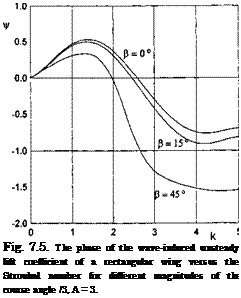
Fig. 7.3. The phase of the wave-induced unsteady lift coefficient of a rectangu­lar wing versus the Strouhal number for different magnitudes of the aspect ratio (dashed lines: small-aspect-ratio approximation (7.31)).

к ~ 4.5, Lw ~ 1.4. These results correlate with the calculated and experimen­tal data of other researchers. According to calculations of Avvakumov [107], obtained by using the method of vortex segments and distribution of sources on wavy ground, the magnitudes of the Strouhal number, corresponding to
the aforementioned minima, were found as к ~ 3 for Л = 2 and к ~ 4.3 for Л = 1. In the work by Shumsky [148], dedicated to the nonlinear flow problem for a two-dimensional foil near a wavy wall (the method of vortex singular­ities in combination with step-by-step linearization in time), the minimum of the unsteady lift was estimated to occur at к ~ 2. In the experimental investigations of Belinsky et al. [149], carried out by using the method of an underwater screen (ground plane), it was shown that for a rectangular wing with an aspect ratio Л = 2, the minimum of the amplitude of unsteady lift occurs at the Strouhal number fc ~ 3.

The solution of problem (7.5)-(7.7) in the general case of an arbitrary angle between the direction of motion of a wing and the wave front was obtained in Rozhdestvensky [57]. A somewhat cumbersome derivation of the solution of this problem and some final closed form expressions for the lift and the moment contributions are given in the Appendix. Note that for oblique waves, the wing is subject to the action of a lateral moment.

In accordance with the general structure of the solution, the wave-induced lateral moment coefficient can be represented in the form

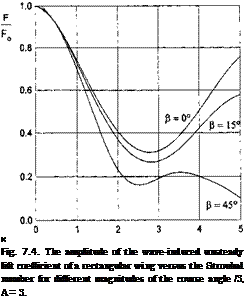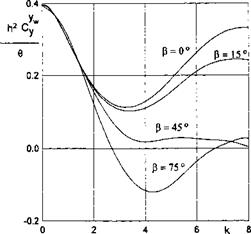
where hi = к cos /3, Fmx (Л, fc, /3) and ^(A, fc, /3) characterize the amplitude and the phase of the lateral moment due to the presence of waves. Some typical results of calculations of the aerodynamic characteristics for oblique waves and a reference point coinciding with the leading edge (a = 1) are plotted in Figs. 7.4-7.7.

Analysis of the results calculated for the wave-induced lift and the lateral

moment coefficients CVw and mXw leads to the following conclusions:

• With an increase in the course angle /3, the minimum of the amplitude of the unsteady lift for a wing of a given aspect ratio decreases and shifts toward the range of longer waves; this shift is more pronounced for wings of a larger aspect ratio;

• Up to the Strouhal numbers corresponding to the minima of the amplitude of the unsteady lift, a phase lag of the lift is observed with respect to the moment of time when the leading edge passes the wave crest. This phase lag vanishes when angle /3 approaches 7t/2 (in the latter case the problem becomes steady, which corresponds to Pmx equal to zero);

• In the range of Strouhal numbers considered, the amplitude curve of the lateral moment coefficient contains two maxima. The magnitude of the first maximum increases when the course angle tends to 7t/2. The position of the maximum shifts toward longer waves with an increase in the aspect ratio.

A* 6 ’

From the general formulas, corresponding to arbitrary course angles, we can derive limiting expressions for a wing of small aspect ratio and wave­lengths much larger than the span:

The amplitude-phase characteristics, corresponding to an unsteady incre­ment of the lateral moment, in the case of wings of small aspect ratio and

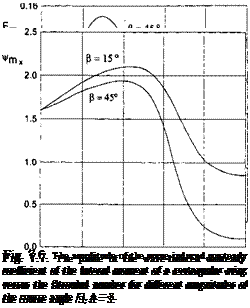long waves take the form

A4fcsin/3 _ 7Г Aft 7Г /‘ъд

_________________ Ф ~ — _j_ — = — – i_ —

192 ’ mx 2 2тг 2 27r*

Turning to the relative wavelength Lw, we obtain the following formula for the amplitude of the lateral moment for A —> 0 and к —> 0:

_ 7rA4sin /3 ЬтПх – 96LW ’

wherefrom it follows that for wings of a small-aspect ratio over long waves, the amplitude of the lateral moment is directly proportional to the aspect ratio to the fourth power and the sine of the course angle and inversely proportional to the relative wavelength.

Because the solutions presented above are linear with respect to the wave amplitude and are valid in practically an unlimited range of Strouhal num­bers, it is possible to apply the Fourier integral to investigate the following:

• motion of a rectangular wing over a cylindrical deformation of otherwise flat ground or over a solitary wave, and influence of a step variation of the ground surface;

• motion of a rectangular wing over a sea surface with irregular waves on it. The solution of the latter problem in conjunction with consideration of the equations of the dynamics of the lifting system in ground the effect opens a possibility of developing the basics of normalization of the seaworthiness and the ride quality of wing-in-ground-effect vehicles.

The asymptotic representation (7.2) of the velocity potential ip can be continued to include the term of the order of O(0a^), which accounts for non­linear effects in the wave amplitude. In this case, the corresponding expansion

_ q-2

for the lift coefficient should be supplemented by the term 6a^ Cya™.

In the simplest case of a wing of infinite aspect ratio A = oo, the expression for this additional term can be obtained in closed form:

Йп2 ~ ~ ~

Су w = A cos 2kt + В sin 2 kt + D

1

4k2 k(l + k2)

-0.4

~ cos 2 к 1 . 7 /7 m 1

+ +,i

The magnitude of D is constant for a given wavelength and characterizes the time-aver aged contribution to the wave-induced lift coefficient. For a positive angle of pitch D > 0.

Calculation by using formula (3.33) shows that for the considered case of a flat plate, a wing flying over sinusoidal waves is subject to action of a constant additional lift increment proportional to the magnitude of the cruise lift coefficient and the square of the ratio of the wave amplitude to the ground clearance.[34]

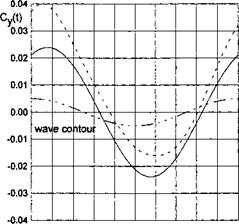
Figure 7.8 presents a history of the wave-induced unsteady lift coefficient related to the cruise lift coefficient Cyo for flying near flat ground with the same relative clearance h.

Calculations were performed by the formula

The calculated data correspond to a wing of infinite aspect ratio (Cyo = 6/h, h —> 0) and relative wave amplitude aw = aw//i = 0.5. The dashed line in Fig. 7.8 describes the wave profile, enabling us to determine the position of the maximum (minimum) of the unsteady lift with respect to the position of the crest or hollow of the wave.

Fig. 7.9. A comparison of theory with experiment for a rectangular wing over waves ( solid lines: theory; circles: experiment [137]; the abscissa of the reference point a = 0.5, Л = 2, k = 1.05).

From a practical viewpoint, for example, for using the results of this solution in the dynamics of flight of a vehicle over waves, it is convenient to represent the aerodynamic coefficients by aerodynamic derivatives of the lift and moment coefficients with respect to the wave coordinate yw and its rate yw.

In this format, the lift and moment coefficients can be calculated with the help of the following formulas:

Cy — Cyo + Cy™yw + yw,	(7.34)
mz = mZ0 + mf1 yw +	(7.35)
mx = mxo + mv™ yw + m%wyw,	(7.36)

where Cyo, mZo, mXo are the cruise values of the aerodynamic coefficients yw = aw cos yw = —к aw sin

Cy„		Cy„	– e <30 ■ ~ K‘-k *■’	(7.37)
myzw	Q = £5 ®m*w.	mfw		(7.38)
m*’w	9 = Д2	m*’	‘ ЇаС’"’-‘	(7.39)

where in all cases, the lift and moment coefficients are defined with respect to the same reference point a. When analyzing the dynamics of the vehicle, this point can be chosen to coincide with the center of gravity. Formulas for

Fig. 7.10. The doubled amplitude of the wave-induced lift coefficient versus the Strouhal number (Л = 2, 0° = 5°,/i = 0.2,aw = 0.1; solid lines: present theory; dashed lines: numerical calculation, [107]).

the above coefficients in the case when the reference point coincides with the trailing edge, are presented in Appendix,[35] Recalculation from the trailing edge to the arbitrary position of the reference point a / 1 can be done by multiplying the complex amplitude of the corresponding coefficient by exp(—fca), see formula (7.22).

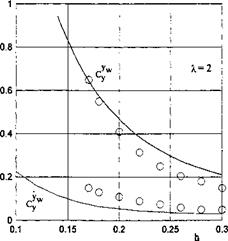
In Fig. 7.9 a comparison is presented of some results calculated for the aerodynamic derivatives with experimental data for motion of a rectangular wing near a wavy solid wall (a = 0.5, Л — 2,0° = 3.3°, (3 = 0, к = k = 1.05). The experiment was conducted by Grebeshov [137] by the method of an underwater screen.

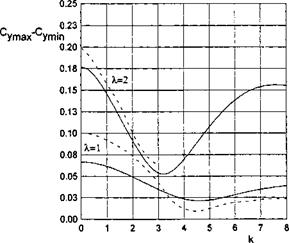
Figure 7.10 presents a comparison of the dependence of the doubled ampli­tude (Cr2/max — СУтіп) of the unsteady lift coefficient versus the Strouhal num­ber with the calculated data of Avvakumov [107] (128 panels on the wing, 720 panels on the ground). In Fig. 7.11 instantaneous magnitudes of the wave – induced lift coefficient of the present theory are compared with calculated data of [107]. Figure 7.12 presents a comparison of results calculated by the present theory with the results of Shumsky [148], where a complete numerical analysis of a two-dimensional inviscid flow past a flat plate above a wavy wall was performed by the discrete vortex technique accounting for the structure of the wake.

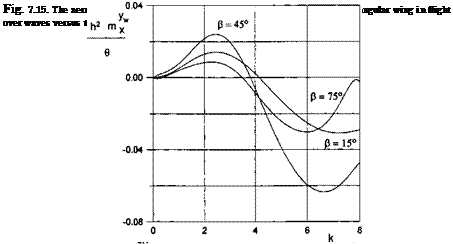
Figures 7.13-7.16 illustrate the influence of the Strouhal number and the course angle upon the aerodynamic derivatives of the lift and the lateral

0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 t/Tw Fig. 7.11. The instantaneous wave-induced lift coefficient of a rectangular wing (A = l, aw = 0.1,h = 0.2,fc = 2.1; solid line: present theory; dashed line: numerical calculation [107]).

Fig. 7.12. The relative influence of the Strouhal number upon the doubled ampli­tude of the wave-induced lift for a flat plate of infinite aspect ratio (A = oo, 9° = 6°,h = 0.2, aw = 0.15; solid line: present theory; dashed line: numerical calculation [148]).

Fig. 7.13. The aerodynamic derivative C^w of the lift coefficient of a rectangular wing in flight over waves versus the Strouhal number for different course angles /3,

A = 2.

0 2 4 6 8

к

Fig. 7.14. The aerodynamic derivative C%w of the lift coefficient of a rectangular wing in flight over waves versus the Strouhal number for different course angles /3, A = 2.

moment coefficients of a rectangular wing of aspect ratio A = 2 in flight over wavy ground. Note that the quantities /i2C^w/0, h2C^w /0, h2m^w/в and к2т%” /0 do not depend either on the relative ground clearance or on the adjusted pitch angle. This feature makes the data representation more compact.

0 2 4 6 8

к

Fig. 7.16. The aerodynamic derivative m^w of the lateral moment coefficient of a rectangular wing in flight over waves versus the Strouhal number for different course angles /З, X = 2.