Our heavyweight helicopter equal in the world does not have
In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]
Perfectly Matching and Stability Consideration
Perfectly matching between the solutions of the PML equations and the linearized Euler equations is one of the most important properties of a PML. It is, however, not obvious from the derivation that the governing PML equation actually possesses this unusual property. Here, it is intended to confirm perfect matching. For this purpose, consider the interface between the Euler computational domain and the vertical PML on the right side of Figure 9.9. If will now be assumed that the computational domain is large compared with the size of the outgoing disturbances, so that the interface may be regarded as infinite in extent in the y direction as shown in Figure 9.10. For convenience, a Cartesian coordinate system centered at the interface will be used. In the Euler domain, the linearized Euler equation (9.35), when written out in full, becomes
dp dp du dv
— + M— I——— 1–
dt dx dx dy
9 u 9 u 9 p
—– + M—– + —
dt dx dx
9 v 9 v 9 p
—– + M—– + —
dt dx dy
9 P d P du dv
— + M— I——— 1–
dt dx dx dy
To allow the most general incident disturbances to impinge on the interface, one may choose to apply Fourier transform in y and Laplace transform in t to Eq. (9.44). This reduces Eq. (9.44) to a system of ordinary differential equations in x in the form (~ over a variable is used to indicate a Fourier-Laplace-transformed variable) as follows:
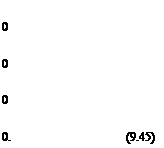. _ . dp du _______
— iojp + M——I—-—+ ifiv =
dx dx
. _ , dU dp)
—io)u + M—— + —— = dx dx
dv)
—iov + M— + їв p = dx
dp) du)
—io p + M— + — + ipv =
dx dx
In Eq. (9.45), в is the Fourier transform variable and o is the Laplace transform variable. Eq. (9.45) is a fourth-order differential system in x. Four linearly
interface
independent solutions can easily be found. They are given as follows:
(a) Entropy waves
й = v = p = 0, /5 = A(p, oi)ei{a/M)x. (9.46)
The amplitude function A (в, o) is arbitrary.
(b) Vorticity waves
p = p = 0, й = Б(в, ш)еі{ш/М)х, v = – щ B(P, oj)ei(a/M)x
The amplitude function Б (в, o) is arbitrary.
(c) Acoustic waves
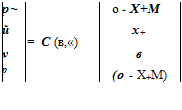
(9.48)
The amplitude function С(в, o) is arbitrary and
 |
 |
 |
 |
 |
 |
-oM + [o2 – в2 (1 – M2)]2
1 – M2
The branch cuts of the square root function in the o plane are shown in Figure 9.11. Eq. (9.48) gives the acoustic waves that propagate or spread to the right. The left propagating acoustic wave solution is obtained by replacing the square root function by its negative value. Note that, for acoustic waves that propagate to the far field, X+ must be real. This requires o2 > в2 (1 – M2). The components for which o2 < в2 (1 – M2) are nonpropagating acoustic near field. They decay exponentially with increasing x.
The most general disturbances that exit the Euler domain on the right side to enter the PML are represented by a combination of entropy, vorticity, and acoustic
Figure 9.11. Branch cuts for the square root function [o2 — в2 (1 — M2 )]1/2 in the complex o plane.
waves. It turns out that the PML equation supports a similar set of wave solutions. The PML equations, Eq. (9.42), when written out in full, are
dp dp d u 9
~dt + M dx + ax + ay(v + U-q-) + U-p + 1 — м2
9 u „9 u 9 p orM
—– + M——- + + uxu + t
dt dx 9 X 1 — M2
9 v 9 v 9 p 9 q4 „x
+ M + + oX —+ axv + – 2 v — 0
dt 9- 9y x dy 1 — M2
9 p d p du dv 9 q3 °xM
+ M + + + U – – + <Jxp + – 2 (u + ^^) = 0
 |
 |
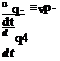dt dx dx 9 y 9 y 1 — M2
The Fourier-Laplace transform of Eq. (9.49) in y and t is
dp du v иx
шр + M + + ївv v — иx + – 2 (p + Mtt) — 0
dx dx xio 1 — M2
du dp ux
—lou + M + + – 2 (u + Mp) — 0
dx dx 1 — M2
. ,dv „ в ux
—lov + +Ів p – U- op + T—Mv = 0
, dp du в ux _ ___
—lop + M + + ifiv — ux v + – 2 (p + Mu) = 0.
d – d – x o 1 — M2
It should be pointed out that at the interface – = 0, the y and t dependence of the transmitted waves must be the same as those of the incident waves. This requires
that в and ш in Eq. (9.50) be the same as those in Eq. (9.45). Eq. (9.50) is a fourth – order differential system in x. The four linearly independent solutions, which can be verified easily, are as follows (a) Entropy waves
 |
|
||
|
|
||
where А(в, ш) is arbitrary. By comparing Eq. (9.46) and Eq. (9.51), it is clear by setting А (в, ш) = А (в, ш) that the entropy wave solution in the PML will match perfectly the entropy wave solution of the Euler domain at the interface x = 0. There is no reflected wave. In addition, Eq. (9.51) indicates that any entropy waves transmitted into the PML will be damped spatially with a damping rate of ax/[M(1 – M2)] in the x direction.
(b) Vorticity waves
|
|
||
|
|||
|
|||
|
|
||
By comparing Eq. (9.47) and Eq. (9.52), it is obvious that by setting B(fi, ш) = В(в, ш), the vorticity waves in the Euler domain are completely transmitted into the PML without reflection at the interface x = 0. In the PML, the spatial damping rate for the vorticity waves is the same as that of the entropy waves.
(c) Acoustic waves
(9.53)
where С(в, ш) is arbitrary and X = X+ + m(l—xM2)[ш2 — в2(1 — M2)]2.
By comparing Eq. (9.48) and Eq. (9.53), it is possible to conclude that there is perfect matching between the acoustic waves incident on the interface at x = 0 and the transmitted acoustic waves in the PML. Perfect matching is achieved by setting С(в, ш) = С(в, ш). This is true not only for propagating acoustic waves for which ш2 > в2(1 – M2), but it is also true for nonpropagating near-field components with ш2 < в2(1 – M2). The spatial damping rate in the PML is equal to ш(1—xM)2 [ш2 — в2 (1 — M2 )]2 in the x direction.
It was mentioned previously that the first version of PML equations were unstable. Now, it is easy to show that PML equation Eq. (9.49) does not support unstable solutions. To prove this assertion, one is required to show that there is no unstable acoustic wave solution in the PML. The simplest way to complete the proof is to take the Fourier transform of Eq. (9.50) in x. Eq. (9.50) is a homogeneous system. It is straightforward to find the condition for nontrivial solution is given by setting the determinant of the coefficient matrix to zero. This gives, after some algebraic simplifications,
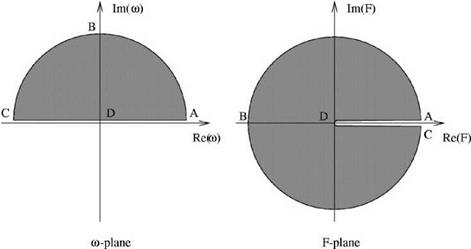
в2
1 — M2’
|
|
|
|
 |
|
|
|
|
|
In Eq. (9.55), a is the Fourier transform variable for x. Eq. (9.54) is the dispersion relation for the acoustic waves supported by the PML equations. To prove that there is no unstable acoustic wave solution, it is sufficient to show that dispersion relation (9.54) has no roots in the upper half ю plane for arbitrary a and в. This can be done by mapping the upper half ю plane into the complex F plane. Figure 9.12 gives the image in the F plane. Notice that there is no value in the upper half ю plane that makes F real and positive. Therefore, Eq. (9.54) cannot be satisfied because the right side of the equation is real and positive. Since both the entropy and vorticity waves are damped waves, PML Eq. (9.49) would only have damped wave solutions.
