Time-Domain Impedance Boundary Condition

Nowadays, acoustic treatment is invariably used on the inside surface of commercial aircraft jet engines for fan noise reduction. Acoustic treatment panels or liners, when properly toned, are extremely effective noise suppressors. Because of structural integrity requirements, the acoustic liners are usually of the Helmholtz resonator type. Figure 10.1 shows a single-layer acoustic liner. The liner consists of a face sheet with holes at a regular pattern. Underneath the face sheet are cavities. The cavities control the frequency range within which damping is most effective. The dominant damping mechanism of this type of liner is attributed to the dissipation arising from vortex shedding at the mouths of the holes (see Melling, 1973; Tam and Kurbatskii, 2000; Tam et al., 2001). The vortex-shedding process converts acoustic energy into the rotational kinetic energy of the shed vortices. These vortices are subsequently dissipated by molecular viscosity. In the absence of vortex shedding, which is the case at a low sound pressure level, the principal damping mechanism is associated with viscous dissipation of the oscillatory flow at the mouths of the Helmholtz resonators. The flow and acoustic fields around the Helmholtz resonators of acoustic liners are exceedingly complicated, especially when there is a mean flow over the liner.

For engineering purposes, a gross macroscopic description of the effects of the acoustic liners on incident acoustic waves is definitely preferred over a more demanding microscopic description of the actual phenomenon. In the aeroacoustic community, it is an accepted practice to characterize the macroscopic properties of an acoustically treated surface by a single quantity Z called the impedance. Impedance is defined as the ratio of the acoustic pressure p to the acoustic velocity component normal to the treated surface vn (positive when pointing into the surface). That is,

P = ZVn. (10.1)

Impedance is a complex quantity, Z = R – iX (e-lmt time dependence is assumed). The use of a complex quantity is needed to account for the damping and phase shift imparted on the sound waves by the acoustically treated surface. The acoustic resis­tance R and the acoustic reactance X are generally frequency dependent. They also vary with the intensity of the incident sound waves and the adjacent mean flow veloc­ity. These quantities are usually measured empirically, although some semiempirical formulas are available for their estimates. It has been found experimentally that R is positive and does not vary much with frequency. On the other hand, X may be

Figure 10.1. A single-layer Helmholtz resonator type acoustic liner.

both positive or negative depending on the frequency. For many acoustic liners, the dependence of X on angular frequency ы can be represented adequately by a simple analytical expression of the following form (Tam and Auriault, 1996):

X _ X-1 + X

—- ———— + Xi ы.

p a0 ы

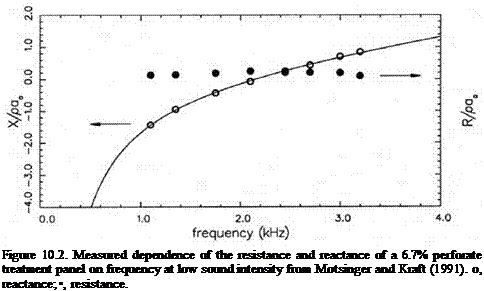
where X-1 and X1 are two parameters, p is the gas density, and a0 is the speed of sound. Figure 10.2 shows an accurate representation of the data of Motsinger and Kraft (1991) by the two-parameter formula. The values of X-1 and X1 obtained by mean-least-square fit are -13.48 and 0.0739, respectively, where ы is measured in kiloradians per second.

The impedance boundary condition (10.1) is basically a boundary condition established for frequency-domain analysis. As it is, it cannot be used in time – domain computation. For time marching computation, a suitable equivalent of the impedance boundary condition in the time domain is needed. One significant advan­tage of time-domain methods over frequency-domain methods is that broadband noise problems can be handled relatively easily, almost without extra effort. For

broadband noise problems, frequency-domain methods are computationally inten­sive and laborious. In addition, if the problem is nonlinear, frequency-domain meth­ods would be exceedingly difficult to carry out.

Time-domain problems can be solved only if they are well posed and stable. In the presence of a mean flow, standard formulation of the impedance boundary condition is known to support spurious unstable solution of the Kelvin-Helmholtz type. It turns out that, for acoustic liner problems, such instability is rather weak. It can be suppressed by the imposition of artificial selective damping at the liner surface.