Local 2D flow quality and singularity models

Near sonic Beltrami equations

The potential equation for a near-sonic plane or axisymmctric flow has a particularly elegant for­mulation in variables of state or in characteristic variables (for details see Ref (78)). illustrating the formal relationship between incompressible, transonic, plane and axially symmetric potential problems: characteristic equation and compatibility relation define a system of quasi-lincar first order differential equations

Here the variables (X. Y) denote the physical space and (U, V) a n<»rmalizcd pair of velocity variables, namely the Prandil-Meyer function and the flow angle. Both pairs are

dependent variables in a workspace ts, t) “Rheograph plane” w hich is identical with characteris­tic variables in supersonic flow (j=l, U>0) and their analytical continuation beyond the sonic – line where j«-1, U < 0. Exponents pt and pj have a switch function: p, =0 denotes plane 2D flow, p, ■ 1 indicates axially symmetric flow; p> = 0 results in a simple mapping of linear sub­sonic or supersonic flow while PS = 1/3 switches to transonic flow. These equations include most of the flow models described by the pioneers in theoretical transomes. in closed analytical form or. for transonic axisyntmetric flow where a weak nonlinearity persists, in a numerically very suitable form

Equations (64M67) describe a large number of educational solutions which should be kept ‘alive’ as part of the knowledge base for transonic design and phenomena analysis. Because of (64)-(67) representing a system for quasi-conformal or characteristic mapping, solu­tions may be interpreted as transformations of geometries consisting of both the boundary con­ditions and ail details of the flow, appearing as an analog flow in the rheograph plane.

Applications of mapped problems to test cases for numerical methods

In the transonic and low supersonic Mach number regime, analytical soloutions describing the local or asymptotic behavior of shock waves in the flow arc of particular interest. Like the well – known logarithmic singularity (79) for the normal shock on a curved contour, there are other sin­gular solutions for interaction of shock waves with solid boundaries or with flow phenomena near sonic conditions. Frequently, limiting cases between two known mathematical models have to be found. One such case is modelling a smooth transition from the mathematically well under­stood far field behavior of an airfoil in some flow * I to the appearance of a detached shock wave in front of it if the free stream М» slightly exceeds unity. This example was solved by a mapping to the rheograph plane (80).

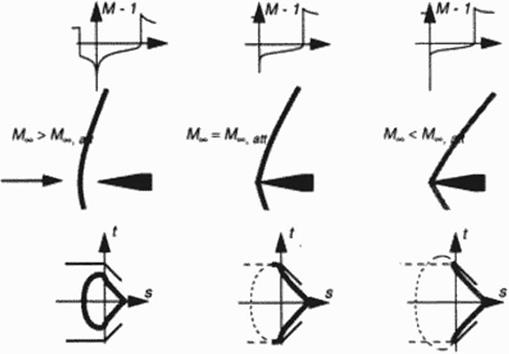
More recently a similar problem was solved by a local mapping of the 2D plane flow near the tip of a wedge ramp at precisely the attachment Mach number The limiting case

between a detached shock, normal to the flow axis, approaching the tip and an oblique shock attached to the wedge in supersonic flow (see the early experiments (81 ]>. had to be found. Fig­ure I illustrates this limiting case both in the physical plane and mapped to the rheograph plane Results arc given in (82). here it’s just worth to mention that another, new logarithmic singular­ity at the wedge tip is found from simple mapping procedures.

The value of such local solutions for new and rerined computational methods in fluid dynamics is evident: known local flow models represent exact solutions and refinements should give information about needed efforts to obtain such solutions numerically to a desired degree of accuracy. The wedge problem serves as a test case for an unstructured grid Euler code [83) where local grid refinements allow for a sharpening of the shock waves occurring in the flow, see Figure 36.