In-Plane H-force

In hover the in-plane H-force, representing principally the blade profile drag, contributed only to the torque. Here, however, since the resultant velocity at the blade is Or + Vsin C (Equation 5.35), the drag force on the advancing side exceeds the reverse drag force on the retreating side, leaving a net drag force on the blade, positive in the rearward direction.

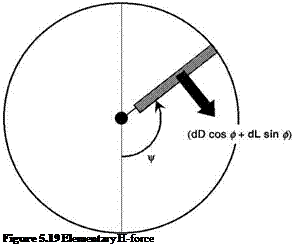
Seen in azimuth (Figure 5.19) the elementary H-force, reckoned normal to the blade span and resolved in the rearward direction, is:

dH = (dD cos f + dL sin f )sin C (5.56)

which may be written as dH0 plus dHi, where the suffices relate to the profile drag and induced drag terms, respectively. Treating the drag term separately and making the usual approxima­tions, we have:

dH0 = dDsinC

In coefficient form, for N blades, this gives:

1 2

pNUj • c • CD0 • sinC dr dCHc = 2 у

2 p(OR)2 pR2

= s • uT • CD0 • sinC dx = s(x + msinC)2 • CD0 • sinC dx

o

— 2 s ■ Cdo ■ m

Overall then for the in-plane H-force, we have:

ch — 2 sCdo ■ m + CHi

Expressions can be obtained for the induced component CHi in terms of У, l, m and the flapping coefficients a0, аг and b: these are derived in varying forms in the standard textbooks, for example Bramwell (p. 148) and Johnson (p. 177). The relations are somewhat complex and since we shall not require to make further use of them in the present treatment, and moreover in the usual case CHi is small compared with CHo, we can be satisfied with the reduction at Equation 5.60.