Biot-Savart Law

Biot-Savart law relates the intensity of magnitude of magnetic field close to an electric current carrying conductor to the magnitude of the current. It is mathematically identical to the concept of relating intensity of flow in the fluid close to a vorticity-carrying vortex tube to the strength of the vortex tube. It is a pure kinematic law, which was originally discovered through experiments in electrodynamics. The vortex filament corresponds there to a conducting wire, the vortex strength to the current, and the velocity field to the magnetic field. The aerodynamic terminology namely, “induced velocity” stems from the origin of this law.

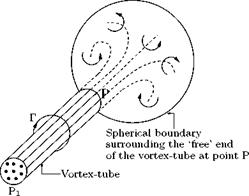
Now let us calculate the induced velocity at a point in the field of an elementary length Ss of a vortex of strength Г. Assume that a vortex tube of strength Г, consisting of an infinite number of vortex filaments, to terminate in some point P, as shown in Figure 5.21.

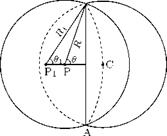
The total strength of the vortex tube will be spread over the surface of a spherical boundary of radius R. The vorticity in the spherical surface will thus have the total strength of Г. Because of symmetry the velocity of flow at the surface of the sphere will be tangential to the circular line of intersection of the sphere with a plane normal to the axis of the vortex tube. Such plane will be a circle ABC of radius r subtending a conical angle 26 at P, as shown in Figure 5.22.

If the velocity on the sphere at (R, 6) from P is v, then the circulation round the circuit ABC is Г’, where:

Г’ = 2nR sin 6 v.

Figure 5.21 Vortex-tube discharging into a sphere.

The radius of the circuit is r = R sin в, therefore, we have:

Г’ = 2nr v.

But the circulation round the circuit is equal to the strength of the vorticity in the contained area. This is on the cap ABCD of the sphere. Since the distribution of the vorticity is constant over the surface, we have:

, Surface area of the cap 2nR2 (1 — cos в)

Г’ = —————————– — Г = ——— 2————– Г,

Surface area of the sphere 4nR2

that is:

(5.43)

B Figure 5.23 A short vortex tube discharged into an imaginary sphere.

From Equations (5.42) and (5.43), we obtain the induced velocity as:

Г

v =——- (1 — cos 9). (5.44)

4лг

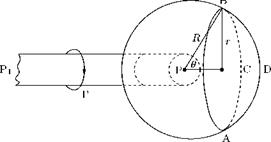
Now, assume that the length of the vortex decreases until it becomes very short, as shown (PjP) in Figure 5.23. The circle ABC is influenced by the opposite end Pj also (that is, both the ends P and P’ of the vortex influence the circle). Now the vortex elements entering the sphere are congregating on Pj. Thus, the sign of the vorticity is reversed on the sphere of radius Rj. The velocity induced at Pj becomes:

Г

vj =——— (1 — cos 9j). (5.45)

4лг

The net velocity on the circuit ABC is the sum of Equations (5.44) and (5.45), therefore, we have:

Ц — cos 9) — Ц — cos 9j)

(cos 9i — cos 9).

As the point Pj approaches P,

(9 — S9) = cos 9 + sin 9 S9

and

(v — vj) ^ Sv.

Thus, at the limiting case of Pj approaching P, we have the net velocity as:

Г

Sv = —- sin 9S9. (5.46)

4лг

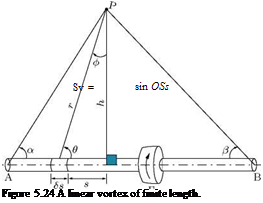
This is the velocity induced by an elementary length Ss of a vortex of strength Г which subtends an angle S9 at point P located by the ordinate (R, 9) from the element. Also, r = R sin 9 and RS9 = Ss sin 9, thus

4nR2

It is evident from Equation (5.47) that to obtain the velocity induced by a vortex this equation has to be integrated. This treatment of integration varies with the length and shape of the finite vortex being studied. In our study here, for applying Biot-Savart law, the vortices of interest are all nearly linear. Therefore, there is no complexity due to vortex shape. The vortices will vary only in their overall length.