Characteristics in 2D and in 3D How

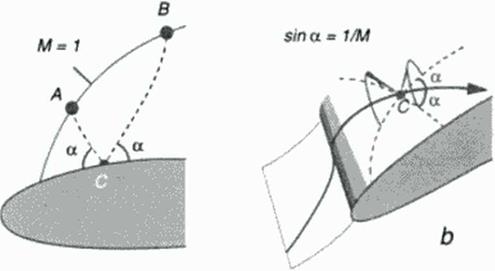
In supersonic flow. Mach waves or characteristics are appearing as straight orthogonal lines ^ = t+s. П * t-s »n the s. i rheograph plane. Basic system (I). or It’s full compressible potential flow extension, see Ref. (86J. maps these families of lines to 2D curses in the physical plane, within the domain of supersonic local Mach numbers Figure 39 shows a 2D airfoil flow clement w ith a chosen surface point C and both characteristics AC and CB intersecting it inclined to the flow direction with an angle a * arcsint 1/M): regions of influence from upstream and dependence to downstream arc defined this way. For given flow data w ithin the sonic line segment AB the so­lution for supersonic flow is completely determined w ithin the triangle ABC This is the basis for the 2D inverse method of characteristics (78) allowing the construction of a supersonic flow pat­tern.

In 3D flow, both families of characteristics are Mach – conoid intersections, as illus­trated in Figure 39b for a 3D wing element. They may intersect the sonic surface far away from surface location C and will not form closed domains comparable to the 2D sonic line interval AB. Mathematically an ill-posed problem, the inverse integration of 3D local supersonic flow fields with a potential flow cross marching technique nevertheless gave very satisfactory results for transonic wings (87). (88). A more recent application for the design of supersonic wings, using an inverse version of the 3D Euler equations is outlined in the next book chapter.