Semi-Infinite Vortex

A vortex is termed semi-infinite vortex when one of its ends stretches to infinity. In our case let the end B in Figure 5.24 stretches to infinity. Therefore, в = 0 and cos в = 1, thus, from Equation (5.49), we have the velocity induced by a semi-infinite vortex at a point P as:

Г

v =—— (cos a + 1). (5.50)

4nh

5.9.1 Infinite Vortex

An infinite vortex is that with both ends stretching to infinity. For this case we have a = в = 0. Thus, the induced velocity due to an infinite vortex becomes:

Г

2nh

For a specific case of point P just opposite to one of the ends of the vortex, say A, we have a = n/2 and cos a = 0. Thus, the induced velocity at P becomes:

Г

4nh

This amounts to precisely half of the value for the infinitely long vortex filament [Equation (5.51)], as we would expect because of symmetry.

While discussing Figure 5.15, we saw that the circulation about an aerofoil in two-dimensional flow can be represented by a bound vortex. We can assume these bound vortices to be straight and infinitely long vortex filaments (potential vortices). As far as the lift is concerned we can think of the whole aerofoil as being replaced by the straight vortex filament. The velocity field close to the aerofoil is of course different from the field about a vortex filament in cross flow, but both fields become more similar when the distance of the vortex from the aerofoil becomes large.

In the same manner, a starting vortex can be assumed to be a straight vortex filament which is attached to the bound vortex at plus and minus infinity. The circulation of the vortex determines the lift, and the lift formula which gives the relation between circulation, Г, and lift per unit width, l, in inviscid potential flow is the Kutta-Joukowski theorem,6 namely:

l =-рГиж, (5.53)

where l is the lift per unit span of the wing, Г is circulation around the wing, иж is the freestream velocity and p is the density of the flow.

It is important to note that the lift force on a wing section in inviscid (potential) flow is perpendicular to the direction of the undisturbed stream and thus an aerofoil experiences only lift and no drag. This result is of course contrary to the actual situation where the wing experiences drag also. This is because here in the present approach the viscosity of air is ignored whereas in reality air is a viscous fluid. The Kutta-Joukowski theorem in the form of Equation (5.53) with constant Г holds only for wing sections in a two-dimensional plane flow. In reality all wings are of finite span and hence the flow essentially becomes three-dimensional. But as long as the span is much larger than the chord of the wing section, the lift can be estimated assuming constant circulation Г along the span. Thus, the lift of the whole wing span 2b is given by:

But in reality there is flow communication from the bottom to the top at the wing tips, owing to higher pressure on the lower surface of the wing than the upper surface. Therefore, by Euler equation, the fluid flows from lower to upper side of the wing under the influence of the pressure gradient, in order to even 6The Kutta-Joukowski theorem is a fundamental theorem of aerodynamics. It is named after the German Martin Wilhelm Kutta and the Russian Nikolai Zhukovsky (or Joukowski) who first developed its key ideas in the early 20th century. The theorem relates the lift generated by a right cylinder to the speed of the cylinder through the fluid, the density of the fluid, and the circulation. The circulation is defined as the line integral, around a closed loop enclosing the cylinder or aerofoil, of the component of the velocity of the fluid tangent to the loop. The magnitude and direction of the fluid velocity change along the path.

The flow of air in response to the presence of the aerofoil can be treated as the superposition of a translational flow and a rotational flow. It is, however, incorrect to think that there is a vortex like a tornado encircling the cylinder or the wing of an airplane in flight. It is the integral’s path that encircles the cylinder, not a vortex of air. (In descriptions of the Kutta-Joukowski theorem the aerofoil is usually considered to be a circular cylinder or some other Joukowski aerofoil.)

The theorem refers to two-dimensional flow around a cylinder (or a cylinder of infinite span) and determines the lift generated by one unit of span. When the circulation Г ж is known, the lift L per unit span (or l) of the cylinder can be calculated using the following equation:

l = рто^тоГто?

where рж and Vж are the density and velocity far upstream of the cylinder, and Г ж is the circulation defined as the line integral,

Г ж = V cos 9ds

around a path c (in the complex plane) far from and enclosing the cylinder or airfoil. This path must be in a region of potential flow and not in the boundary layer of the cylinder. The V cos 9 is the component of the local fluid velocity in the direction of and tangent to the curve c, and ds is an infinitesimal length on the curve c. The above equation for lift l is a form of the Kutta-Joukowski theorem.

The Kutta-Joukowski theorem states that, “the force per unit length acting on a right cylinder of any cross section whatsoever is equal to PжVжГж, and is perpendicular to the direction of Vж”
out the pressure difference. In this way the magnitude of the circulation on the wing tips tends to become zero. Therefore, the circulation over the wing span varies and the lift is given by:

■+ b

Г(х) dx,

b

where the origin is at the middle of the wing, x is measured along the span, and b is the semi-span of the wing.

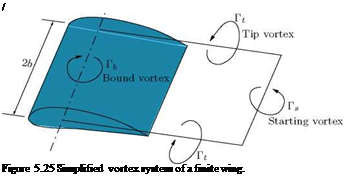
According to Helmholtz’s first vortex theorem, being purely kinematic, the above relations for lift are also valid for the bound vortex. Thus, isolated pieces of a vortex filament cannot exist. Also, it cannot continue to be straight along into infinity, where the wing has not cut through the fluid and thus no discontinuity surface has been generated as is necessary for the formation of circulation. Therefore, free vortices, Г, which are carried away by the flow must be attached at the wing tips. Together with the bound vortex, Гь, and the starting vortex, Ts, they (the tip vortices) form a closed vortex ring frame in the fluid region cut by the wing, as shown in Figure 5.25.

If a long time has passed since start-up, the starting vortex is at infinity (far downstream of the wing), and the bound vortex and the tip vortices together form a horseshoe vortex.

Even though the horseshoe vortex system represents only a very rough model of a finite wing, it can provide a qualitative explanation for how a wing experiences a drag in inviscid flow, as already mentioned. The velocity w induced at the middle of the wing by the two tip vortices accounts for double the velocity induced by a semi-infinite vortex filament at distance b. Therefore, by Equation (5.50), we have:

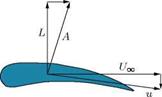
This velocity is directed downwards and hence termed induced downwash. Thus, the middle of the wing experiences not only the freestream velocity Ux, but also a velocity u, which arises from the superposition of Ux and downwash velocity w, as shown in Figure 5.26.

In inviscid flow, the force vector is perpendicular to the actual approach direction of the flow stream, and therefore has a component parallel to the undisturbed flow, as shown in Figure 5.26, which manifests itself as the induced drag Di, given by:

w

Di — A.

U

It is important to note that Equation (5.57) holds if the induced downwash from both vortices is constant over the span of the wing. However, the downwash does change since at a distance x from the wing center, one vortex induces a downwash of:

Г

4 n (b + x) ’

whereas the other vortex induces:

Г

4 n (b — x)

Both the downwash are in the same direction, therefore adding them we get the effective downwash as:

ГГ w — +

4 n (b + x) 4 n (b — x)

_ Г 2b

4 n b2 — x2

_ Г b

2 n b2 — x2

From this it can be concluded that the downwash is the smallest at the center of the wing (that is, Equation (5.57) underestimates the induced drag) and tends to infinity at the wing tips. The unrealistic value there (at wing tips) does not appear if the circulation distribution decreases towards the wing tips, as in deed it has to. For a semi-elliptical circulation distribution over the span of the wing, the downwash distribution becomes constant and Equation (5.57) is applicable. Helmholtz first vortex theorem stipulates that for an infinitesimal change in the circulation in the x-direction of:

dT

dr — dx dx

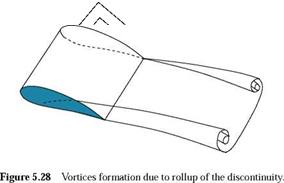
and a free vortex of the same infinitesimal strength must leave the trailing edge. This process leads to an improved vortex system, as shown in Figure 5.27.

The free vortices form a discontinuity surface in the velocity components parallel to the trailing edge, which rolls them into the kind of vortices, as shown in Figure 5.28.

These vortices must be continuously renewed as the wing moves forward. This calls for continuous replenishment of kinetic energy in the vortex. The power needed to do this is the work done per unit time by the induced drag.

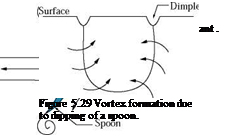
The manifestation of Helmholtz’s first theorem can be encountered in daily life. Recall the dimples formed at the free surface of coffee in a cup when a spoon is suddenly dipped into it. The formation process of dimples looks like that shown schematically in Figure 5.29.

As the fluid flows together from the front and back, a surface of discontinuity forms along the rim of the spoon. The discontinuity surface rolls itself into a bow-shaped vortex whose endpoints form the dimples on the free surface, as shown in Figure 5.29.

The flow outside the vortex filament is a potential flow. Thus, by incompressible Bernoulli equation, we have:

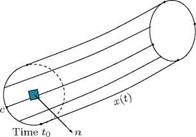
Figure 5.30 A closed curve on a vortex ring at times to and t.

This is valid both along a streamline and between any two points in the flow field.[5] Also, at the free surface the pressure is equal to the ambient pressure pa. Further, at some distance away from the vortex the velocity is zero and there is no dimple at the free surface, and hence z = 0. Thus, the Bernoulli constant is equal to pa and we have:

2

2 pu + pgz = 0.

Near the end points of the vortex the velocity increases by the formula given by Equation (5.52), and therefore z must be negative, that is, a depression of the free surface. In reality, the cross-sectional surface of the vortex filament is not infinitesimally small, therefore we cannot take the limit h ^ 0 in Equation (5.52), for which the velocity becomes infinite. However, the induced velocity due to the vortex filament is so large that it causes a noticeable formation of dimples.

It should be noted that an infinitesimally thin filament cannot appear in actual flow because the velocity gradient of the potential vortex tends to infinity for h ^ 0, so that the viscous stresses cannot be ignored even for very small viscosity. Also, it is well known that the viscous stresses make no contribution to particle acceleration in incompressible potential flow, but they do deformation work and thus provide a contribution to the dissipation. The energy dissipated in heat stems from the kinetic energy of the vortex.