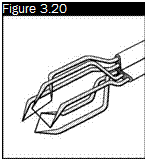
Triaxial probe

To determine the three-dimensional velocity vector, a set of three mutually perpendicular sensors, the triaxial probe of Figure 3.20, is needed to allow measurement in a cone of 70° around the axis of the probe.

Velocity components are calculated from the voltages measured at the three wires by using velocity curves obtained by calibration. The speeds on the three wires are obtained by equations:

k<u< + u2 + h1u3 = (l + k1 + h1 )cos 35.3°ucal1

k<u< + k2u2 + u3 = (l + k2 + h2)cos 35.3°ucal1

u<T h3 u2 + k3u3 = (1 + k3 + h3 )cos 35.3°uCal3

Putting, for simplicity, the values of h and k for all wires equal to those provided by the manufacturers, the velocity components in the direction of three sensors can be found from the equations:

u ^/-0.3676u2ali + 0.3747u2al2 + 0.3453u2al3

u2 = y]0.3453u2Ca/i – 0.3676uil2 + 0.3747ui/3

u3 =40.3747u2Cai + 0.3453u;al2 – 0.3676u2al3

Triaxial probe

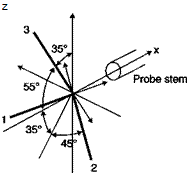
Finally, the three components of the velocity vector in the coordinate system of the probe can be calculated from the equations:

u = u1 cos54.74° + u2 cos54.74° + u3 cos54.74°

v = – u1 cos 45° – u2 cosl35° + u3 cos 90°

w = – u1 cos114.09° – u2 cos114.09° – u3 cos35.26°