Local Flow Problems for Analysis of PAR Mode
Notwithstanding a certain degree of idealization, the scheme with the reentrant jet (scheme 1) gives the possibility of obtaining the results which are sufficiently plausible and compatible with experimental data on PAR efficiency. We consider some relevant local problems of flows around the leading and trailing edges. Solutions of these problems were obtained by Fridman [157] by the method of S. A. Chaplygin of singular points within the frame of the ideal jet theory.
8.1.1
 |
Reentrant Jet Flow Near the Leading Edge
We consider scheme 1 of the power-augmented flow past a wing in the extreme ground effect. We introduce stretched local coordinates near the leading edge as
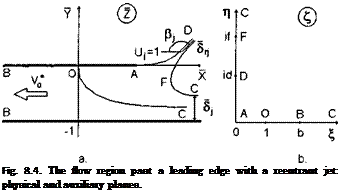
where hi = h*( 1) is a local ground clearance at the leading edge and Ls is the stretched distance of the stagnation point from the tip of the leading edge. The plane of physical flow is depicted in Fig. 8.4.
Assume as known the width of the incoming jet 5j and the velocity on its boundary C/j = 1. To determine the relative velocity potential of the flow, we apply the method of singular points of S. A. Chaplygin, which employs the idea of determining a holomorphic function in the complex plane, knowing the function’s zeros and poles and applying Liouville’s theorem; see Gurevich [138].
We map the domain of the flow in the physical plane z = x + iy onto the first quadrant of an auxiliary complex plane £ = £ + irj, so that the solid boundary AOBC of the flow in the Z plane is transformed into a positive semiaxis £ > 0 and the free surface part ADFC of the boundary in the physical plane be transformed into a positive semi-axis rj > 0. Taking into consideration that the complex conjugate velocity in the physical plane dw/dZ has a zero of the first order at the stagnation point (£ = 1) and performing an analytic continuation of this function onto an entire plane £, we obtain
![]() d w £ — 1
d w £ — 1
dz=‘cTT
The complex conjugate velocity of the flow in the auxiliary plane £ is found as
dw = ДГ C(C2 – 1) dC (C2+d2)(C2-62)
![]() Expression (8.2) can be commented on in the following way. The complex potential w should have a zero of the second order at the point ( = 1, that is, w = 0[(£ — l)2]. Because there is no violation of conformity at this point, the complex conjugate velocity may be assumed to be dw/d( = 0(£ — 1), i. e., having a simple zero at ( = 1. At the point ( = id, which is the image of infinitely distant point D of a free jet, the function dw/d( must have a pole of the first order (a stream with a finite flow rate). Physically, such behavior corresponds to that of a sink in an auxiliary plane and models the disappearance of the jet on the second leaf of a Riemann surface. In addition, the function dw/d( has another simple pole at the point ( = 6, which corresponds to a stream of a finite flow rate inside the channel. The resulting expression (8.2) was found by analytic continuation of singular points of the function dw/dC with the subsequent application of the Liouville theorem.
Expression (8.2) can be commented on in the following way. The complex potential w should have a zero of the second order at the point ( = 1, that is, w = 0[(£ — l)2]. Because there is no violation of conformity at this point, the complex conjugate velocity may be assumed to be dw/d( = 0(£ — 1), i. e., having a simple zero at ( = 1. At the point ( = id, which is the image of infinitely distant point D of a free jet, the function dw/d( must have a pole of the first order (a stream with a finite flow rate). Physically, such behavior corresponds to that of a sink in an auxiliary plane and models the disappearance of the jet on the second leaf of a Riemann surface. In addition, the function dw/d( has another simple pole at the point ( = 6, which corresponds to a stream of a finite flow rate inside the channel. The resulting expression (8.2) was found by analytic continuation of singular points of the function dw/dC with the subsequent application of the Liouville theorem.
Dividing left and right sides of formula (8.2) by corresponding sides of formula (8.1) and integrating the resulting expression taking into account the requirement Z( 1) = 0, we obtain the relationship between the planes Z = Z(C) in the form
N Si (C2^2)(C2-62)dC – ^
We find the constants
ъ-т-и-н [ (M
The condition of mass conservation is given by2

 |
wherefrom _
*rj К
і + <p b2 -1′
The requirement, accounting for angle /?j of orientation of the reentrant jet, is
^J(id) = exp[-(7T – $)i] = b-L (8.9)
 |
The flow velocity on AB (the “wetted” surface of the wing), ( = £, 77 = 0, f Є [0,6), is
![]()
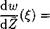
where £ is determined from
The solution derived herein gives the possibility of calculating the local pressure distribution on the wing and the ground near the leading edge, as well as the inclination angle /?j and the flow rate of the reentrant jet as functions of the flow rate of the incoming jet and the elevation of the leading edge above the ground.











