Numerical Examples

To illustrate the implementation and the effectiveness of multi-size-mesh multi­time-step computing, two problems from the Third CAA Workshop on Benchmark Problems are considered here. The first is a two-dimensional rotor noise problem. The second is an automobile door cavity tone problem.

12.4.1 First Example: The Sound Field of an Open Rotor

For this problem, it is convenient to use nondimensional variables with respect to the following scales:

length scale = b(length of blade) velocity scale = a0 (ambient sound speed) time scale = b/a0

density scale = p0 (ambient gas density) pressure scale = p0 a0

body force scale (per unit volume) = p0a200/b

A rotor (see Figure 12.10) exerts a rotating force on the fluid. As a model problem, the rotor is replaced by a distribution of rotating body force. The governing equations are the linearized Euler equations. In cylindrical coordinates (r, ф, x), they

are as follows:
F (r x) I F (x)rJm (XmNr), r < 1 ^x) 0 r > 1
(12.30)
(12.34)

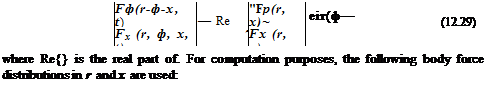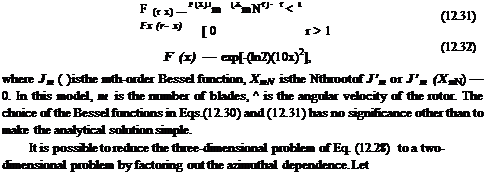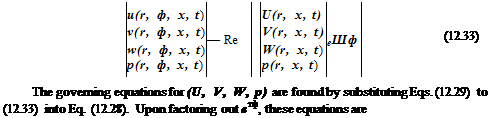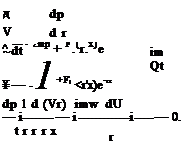For an open rotor solution, it is only necessary to find the outgoing wave solution of Eq. (12.34) in the r – x plane.

Now, the benchmark problem is to calculate the directivity, D (в), of the radiated sound for a eight-blade rotor (m = 8) with N = 1 (Л8д = 9.64742). In a spherical polar coordinates system (R, в, ф), with the x-axis as the polar axis, the directivity is defined by

D(e) = lim R2p2 (R, в, ф, t),

where an overbar indicates a time average. The directivity D(e) at one-degree inter­val at two rotational speeds

(a) ^ = 0.85 (subsonic tip speed)

(b) ^ = 1.15 (supersonic tip speed)

are to be computed.

To ensure that the computed solution is accurate, one must make provisions to take into account two important characteristics of this problem. First, the noise source is discontinuous at the blade tip. This could be a source of short spurious numerical waves. Second, the blades are slender, that is, the loading is concentrated over a narrow width. Computationally, this requires a finer spatial resolution in the source region than in the acoustic radiation field.