Crossed-beams (or interference) LDA
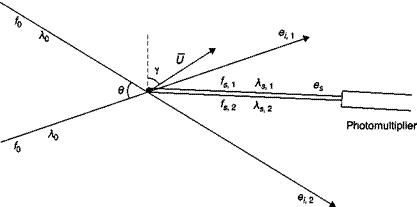 |
This system represents an improvement on the previous one and is also easier to be interpreted. The moving particle is illuminated by two light beams of equal intensity (Figure 4.11) obtained from splitting one laser beam. The particle scatters the light from each of the two beams: from
beam 1, with wavelength 1s1 and frequency fs1, and from beam 2, with wavelength 1s2 and frequency fs2.
Using Equation (4.3):
f1 = f0 +UU ■ (s – e,1) f2 = f0 +^’ (s e’2 )
Since, as we have seen, the variable part of the photomultiplier signal is only due to the difference of the frequencies, the Doppler frequency, we have:
f f2 – fsі =-^- (i – e2) (4.6)
From this equation some important conclusions can be inferred:
■ The frequency fD of the output signal of the photomultiplier is directly proportional to the velocity component (Ucosy normal to the bisector of the angle в formed by the two incident beams).
■ The frequency fD is independent of the direction of observation: this allows great freedom in the choice of configuration (forward – and back-scatter), and furthermore, allows the scattered light to be captured at a large solid angle and focused on the surface of the photomultiplier that therefore receives a much higher light intensity than in the reference beam system: a less powerful laser can be used.
■ The frequency fD can be made convenient for signal processing by an appropriate choice of the angle в between the two incident beams.
The crossed-beam system can be analyzed in a different way that leads to the interference principle. Consider the area where the two beams intersect (Figure 4.12): there are two beams of laser light from the same source coherent and with the same wavelength, l, and the same intensity I1 = I2 = I. By Equation (4.5):
![]() /1+2 = 2/[1 + cos (a1 – a2)] = 2I
/1+2 = 2/[1 + cos (a1 – a2)] = 2I
Since the pairs of interfering beams have different paths, the light intensity of their sum will vary with the difference in path lengths. The extreme cases are:
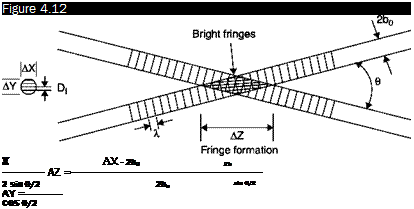 |
Formation of interference fringes in the measuring volume of a crossed-beams LDA
Source: [1]
■ the difference in path lengths is equal to a multiple of the wavelength, f1 – f2 =N1 (N = 0, ±1, ±2….): the resulting light intensity is I1+2 = 47;
■ the difference in path lengths is equal to an odd multiple of half wavelengths, f 1 – f 2 = (2N + 1) 1/2: the resulting light intensity is zero, 71+2 = °.
In the area of intersection of the two laser beams, which is the measurement volume, a series of parallel interference fringes is generated; the distance between two consecutive fringes is:
![]() Я
Я
![]() 2 • І в 2sinl — ‘ 2
2 • І в 2sinl — ‘ 2
When a particle crosses the measuring volume, it is illuminated by a light variable with the Doppler frequency, recalling Equation (4.4):
so the velocity component normal to the fringes can be calculated by measuring the Doppler frequency and the distance between the fringes.
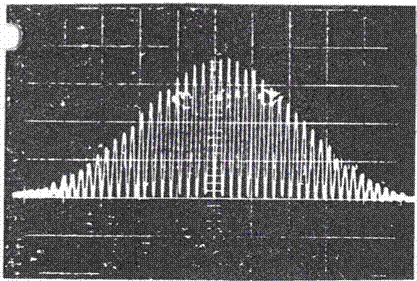 |
The trace on an oscilloscope of a typical signal is shown in Figure 4.13: since the laser beam has a Gaussian intensity distribution of light, even the signal has the same trend.
The angle of intersection of the two beams should be chosen so that the distance between two adjacent fringes is 10 pm. For Equation (4.9), this leads to signal frequencies of 50 MHz for a velocity component of 500 m/s. The precision with which the velocity of the particle can be measured knowing the Doppler frequency depends on the accuracy with which the distance between the fringes can be measured; the measurement can be done by projecting the magnified image of the fringes together with a microscopic net inserted in the control volume.
If the flow is turbulent (zone of separation, wakes, etc.), speed can be null or of unknown direction. The zero speed is not recognized because there is no output signal from the photodetector, the direction of the velocity component cannot be inferred from Equation (4.9) since the Doppler frequency is independent of the sign of the velocity component.
This ambiguity can be eliminated by passing one of the beams through a Bragg cell, which is an acoustic-optical modulator (Figure 4.14) consisting of a crystal or a liquid, transparent, to which a vibrator (a piezoelectric transducer) sends a pressure wave, and then a wave of an index of refraction with a constant frequency, typically 40 MHz. For the
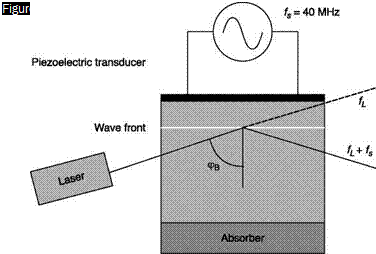 |
laser beam passing through the cell, this is a change of optical path with the same frequency of the vibrator.
At the intersection of the two beams, the interference fringes are apparently moving in the direction orthogonal to the fringes themselves with a speed that has to be algebraically summed to the particle velocity component normal to the fringes. In particular, a steady particle, due to the moving fringes, emits a signal with the frequency of 40 MHz; if the velocity of the particle is concordant or discordant with the motion of the fringes it will give a signal with a frequency less or greater than 40 MHz.
In another interpretation it can be said that the Bragg cell changes the frequency of the beam (frequency shift) that crosses it, giving rise to a constant Doppler signal which acts as a carrier for the signals generated by the moving particles.













