Unseparated Flows Near Leading and Trailing Edges

The local flows near the leading and trailing edges for the conventional (with­out power augmentation) cruise of a wing-in-ground-effect vehicle were con­sidered in sections 2 and 3. Here attention is paid to some local problems that describe the unseparated flows near the leading and trailing edges of the wing in the power-augmented mode, when the incoming and (or) escaping stream has a finite width.

8.1.2 Unseparated Coanda Flow Past a Leading Edge

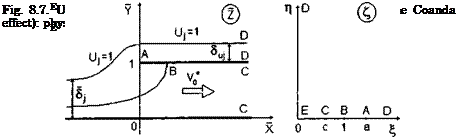
This regime of flow in the power-augmented mode was observed experimen­tally in [153, 155, 156] and represents a practical interest from the viewpoint of enhancing the efficiency of takeoff. The corresponding flow pattern and auxiliary plane £ are shown in Figs. 8.7, with

1-х

hi ’

where hi is a the local elevation of the leading edge above the ground (the leading edge relative to the ground clearance).

The approach for deriving the solution is similar to that applied in previ­ous sections. In what follows, the main results of this solution are presented.

The complex conjugate velocity and the potential derivative in the auxiliary plane £ are dw £ — 1 £ + a dZ ~ C + l C-o’ (8.47) dw – N-?-1 dC C(C2-c2)’ (8.48) Therefore, z(0 = ^ dZ dw (C + l)2 С_а, л. /« dwdCdC~N L C(C2-c2) C + adC + 1- (8.49) The unknown parameters can be found from the following conditions * dw 1 — с a + c V° = d.2(c)= 1+c a — c (8.50) n 1 I dw АҐ nN X (8.51) ^ 1 IdvJJS 7гАГ(с2-1) , Q° = -2i ZdCdC=“ 2c2 (8.52) The flow rate of air should remain the same far downstream, i. e., Qe = Qd + Qc, (8.53) where II Q Q> (8.54) Therefore,

Equations (8.50), (8.51), (8.52), and (8.53) enable us to determine four constants out of five. The fifth unknown, u*, is determined from the procedure of matching. Due to the circulatory flow at the leading edge a suction force occurs (the image of the tip of the leading edge in the ( plane is located at a point £ = a, ?7 = 0). The suction force coefficient can be derived by singling out the intensity of the square root singularity at the leading edge.

For C -> a,

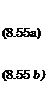d w л a — 1 1

—=r ~ 2 a————— ,

d Z a-f 1 £ — a

(a+ 1)2

4a2(a2 — c2)

is the intensity of the square root singularity. The coefficient of the suction force in 2-D flow is given by

Cs = 2тг A2. (8.57)

The parameters contained in the formula for A are found in the form

It is easy to see that this result coincides with formula (4.62) with U(t) = 1 (steady flow). Thus, it turns out that within the assumption Suj = 0(1), the suction force acting on the leading edge in a flow of finite width is identical to that for unlimited flow.

We write the asymptotic expansion of the function dw/dZ (the complex conjugate velocity) in more detail. From (8.47) for ( a,

Based on this expression, we can single out a constant component of the horizontal velocity near the leading edge,

a2 + 4a – 1

U’ = ~(^+W~

Taking into account (8.47)-(8.49), the velocity and pressure coefficient in the local flow problem can be determined by the following formulas valid on AB: £ = £; £ є [a, oo), ri = 0,

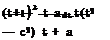
where