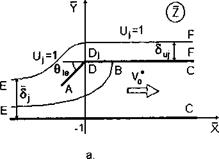
Coanda Flow of Finite Width Past a Deflected Leading Edge

This local problem is of interest in connection with the possibility of in­creasing the reserve of efficiency of the power-augmented modes by providing shock-free entry of the tip of the leading edge. The scheme of the flow and the auxiliary plane are shown in Fig. 8.8, where x = (x — l)/h, у/hi, hi = h( 1), and Ъы is the length of the deflected part of the leading edge as a fraction of the leading edge ground clearance h. Here are the main steps and the results of the solution obtained by the method of singular points of S. A. Chaplygin. The complex conjugate velocity in the auxiliary plane can be derived in the form

d w + C + dx’W71′

dZ ^ CTb C-a 4 + 1 C-d)

Fig. 8.8. Flow of finite width around the leading edge with a deflected tip (the Coanda effect): physical and auxiliary planes.

The derivative of the complex velocity potential in the auxiliary plane is
dw = C2 ~ b2 dC C(C2-c2)’
(8.66)
Mapping of the physical plane onto the auxiliary plane is realized by the function
c d£dw cb dC d<*
(< + b)2 С-о /С + 1 C^de’e/7r dt C(C2-c2) C + a 4-1 t + d)
= N	(8.67)
Unknown quantities are determined from the following conditions:
1 Г dw 7ГNb2 – QE = Tit dc=^ = <i’
(8.68) (8.69)
-^(c2. 2c2 1
b2)
From mass conservation,
Qe = Qd + Qc, where Qd = SUy It follows from the preceding relationships that <Suj = Qe — Qc = Prom (8.69), (8.70) we can find that	(8.70)
(8.71) (8.72) (8.73) (8.74) (8.75)
$
In addition
— F—— —)le/ dt = 0, q, t — 1 d t’
(8.76)

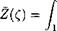
d£ — ^ief*

t(t2 — c2) a + t t — 1 d + ts The magnitude of v* is determined by matching. For the remaining six unknowns, six equations are obtained, namely, (8.68), (8.71), (8.72), (8.73), (8.76), and (8.77). Accounting for the relationships

v*0 + M v* — M ’

a — c

where

л/г b — c fl—cd–ceie/n
b = c/ ^l-v*/5h

we can reduce this system to one containing three unknowns a, c, and d and including equations (8.76), (8.77), and the additional condition

M – V* = 0. (8.78)

a — c

The suction force at point A can be determined by the formulas of S. A. Chaplygin

die dw

dZd? dc’

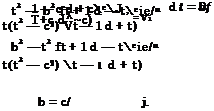Consideration of the last formula shows explicitly that it is possible to choose an angle of deflection of the leading edge tip that corresponds to shock-free entry, that is, zero suction force. This takes place at a = b. For a given length of the deflected part of the edge (forward flap) 6ief, this angle can be determined from the solution of the system

The normal force coefficient for the deflected part of the leading edge normalized with respect to bef is

N fd (t-b)2 t-a (t-l d + te’°/* ,

Ji t(t2 – c2) t + l ІГЙ cT^t)

and for zero suction force,

_ N_ fd t2~b2 (1~ 1 Af

П° Ъы Ji t(t2 — c2) t + ld — t)