Stream-Function-Coordinate (SFC) Concept
One of the fastest known inverse design techniques is based on a stream function formulation 1142]. The inviscid. compressible, steady flow around a given 3-D configuration can be predicted by solving for two stream functions. ЧЧк. у.г) and A(x. y.z) (I42)-| 146) (Figure 70). For the purpose of inverse shape, design this formulation can be inverted. That is. two quasi-lincar second order coupled partial differential equations of the mixed elliptic-hyperbolic type can be derived These two equations treat the x-coordinate and the values of Ч'(х. уд) and A(x, y.z)or their derivatives as known quantities on the, as yet. unknown solid surface of the 3-D configuration, while treating values of у = y(x,4#.A) and r = /.(х. Ч’.Л) for every 3-D streamline as the unknowns Thus, the result of a numerical integration of this inverted system are the y-and-z coordinates of the 3-
D streamlines. Those streamlines that correspond to the specified surface values of Ч'(х. уд) and Л(х, уд) are recognized as the desired 3-D aerodynamic configuration.
|
|
|
|
– jtVv * VXuM – (J4a – f/f A – !(*, – v, X*i ~ *.)!
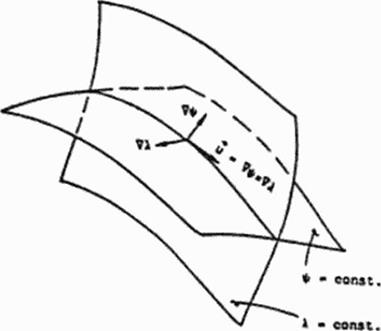
Figure 70 Geometrical interpretation of mass flow rate through a stream tube bounded by two pairs of stream surfaces (144).
A computer code that implements this technique converges very fast because it implicitly satisfies mass at every iteration step thus avoiding the need for integrating the mass conservation equation. Moreover, such a code can be executed in an analysis mode when Dirichlet boundary conditions for ЧЧх. уд) and A(x. y.z) arc specified at every surface point, or in its inverse design mode when Neumann boundary conditions for H^tx. y.z) and A(x. y.z) are specified at every yet unknown surface point. Despite its remarkable speed of execution, robustness and the fact that the entire field of 3-D streamlines is obtained as a by-product of the computation. the SFC concept has its serious disadvantages. This inverse design method requires development of an entirely new code for the solution of the two Strcam-Function-as-a-Coordinate (SFC) equations. The method is not applicable to viscous flow models, it suffers from the difficulties of the geometric muluvaluedness of the stream functions, and is analytically singular at all of the points where die Jacobian of transformation fF. A.Oy (x. yz) become /его (I42J. This occurs ai every point where the x-component of the local velocity vector is zero which can happen at a number of points whose locations we do not know in advance. Consequently, the SFC method is recommended only for the inverse design of smooth 3-D configurations where preferably there arc no stagnation points (3-D duct (146]) or where we are willing to neglect the designed shape in the vicinity of the leading and trailing edges