Order Constraints

For small A, it is often desirable to require interpolation formula (13.4) to be accurate to a specified order of Taylor series expansion in A. This requirement imposes a set of constraints on the interpolation coefficients Sj. To find these constraints in their simplest form, first expand f(x, y) about (xo, yo) to obtain

On substituting (13.24) into (13.4), it is found that

N

y ixoi y0)=y ixoi y0^: sj

Thus, if Eq. (13.25) is truncated to order AM, Sj must satisfy the following conditions:

N

J2sj = 1, M = 0 (13.26)

j=1

N

J2 ixj – xo)p(yj – yo)qsj = °> 1 < p + q < M• (13.27)

j=1

From Eq. (13.25) it is easy to see that, if the order of truncation is increased from (M – 1) to M, (M + 1) more constraints are added. Therefore, the total number of constraints, T, to be satisfied, if Eq. (13.24) is truncated at the Mth order, is

T = 1 + 2 + 3 + ••• + (M + 1) = 1 (M + 1)(M + 2). (13.28)

It is possible if (x/, yj), j = 1,2,…, N are points on a highly regular grid, the total number of independent constraints given by Eqs. (13.26) and (13.27) is less than that calculated by Eq. (13.28). Degeneracy would occur when a number of x/s or y/’s are the same. In this case, only the linearly independent constraints need to be imposed.

Now for a given interpolation stencil with a given set of points (x;-, y;-), j = 1,2,…, N, the interpolation coefficients Sj for the point (xo, yo) may be found by minimizing the total error E2 given by Eq. (13.9), subjected to order constraints (13.26) and

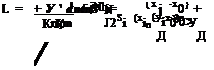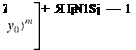(13.27). This constrained minimization problem can again be easily solved by the method of Lagrange multipliers. Let

where n, m = 0,1,2,…, M; n + m < M; n and m are not both equal to zero. M is the order of truncation and дmn are Lagrangian multipliers. Since the total number of constraints (T as given by Eq. (13.28)) cannot exceed the number of stencil points, it is understood that T < N. The conditions for a minimum are as follows:

Again, Eqs. (13.30) to (13.32) lead to a linear matrix equation for the unknowns Sj, Я, and дmn. Let the transpose of the vector X and d be defined by

where bj’s are given by Eqs. (13.20) and (13.21). It is easy to establish by means of Eqs. (13.30) to (13.32) that X is the solution of the matrix equation

(13.35)

The coefficient matrix B may be partitioned into four submatrices as

A is a (N + 1) by (N + 1) square matrix. It is the same as that of Eq. (13.15). C is a (N + 1) by (T — 1) matrix. Ct is the transpose of C. The zero matrix 0 is a square matrix of size (T — 1). On writing out in full, the elements of matrix C are as follows:

"(x — X0 )

(У1

— y0)

(X1 — X0 )2

(X1

— X0 )(УГ

-y0)

(У1

— У0 )2

X — X0 )3

(X1

— X0 )2 (У!

— y0) ■

– (X!

– X0)У

У0 )M-1

(y1

X — X0 )

(У2

— y0 )

(X2 — X0 )2

(X2

— X0)(y2-

-y0)

(У2

— У0 )2

(X2 — X0 )3

(X2

— X0)2 (У2

— y0) ■

– (X2

– X0)(y2 —

У0 )M-1

(y2

c =

X — X0)

(Уі

— y0 )

(Xj — X0 )2

(Xi

— X0 )У-

-y0)

(Уі

— У0 )2

(Xj — X0 )3

(Xj

— X0)2 (Уі

— y0) ■

(Xj

– X0)(Уі –

У0 )M-1

(Уі

(XN — X0 )

(yN

— y0 )

(Xn — X0 )2

(XN

— X0 )(yN

— y0 )

(yN

— У0 )2

(Xn — X0 )3

(XN

— X0 )2(yN

— y0) ■

■■ (XN

– X0 )(yN

– У0 )M-

(yN

0

0

0

0

0

0

0

-У0 )M" -У0 )M -У0 )M. – У0 )M 0

(13.37)

Again, once Eq. (13.35) is solved, the interpolation coefficients Sj’s are found. By substituting the values of Sj’s into Eq. (13.8), the local interpolation error, £local, at wave number (а А, в A) may be computed.