Reynolds Number Effects on the LEV and Spanwise Flow: Hawkmoth, Honeybee, Fruit Fly, and Thrips in Hovering Flight

As discussed previously, the lift enhancement due to the delayed stall of the LEV is important in flapping wing flight [199] [245]. The formation of the LEV depends on the wing kinematics, the details of wing geometry, and the Reynolds number [397]. To examine the Re effect on LEV structures and spanwise flow for insect-like wing body configurations with appropriate kinematic motions, Shyy and Liu [397] and Liu and Aono [225] investigated the flapping wing fluid physics associated with the hawkmoth (Re = 6.3 x 103, k = 0.30), honeybee (Re = 1.1 x 103, k = 0.24), fruit fly (Re = 1.3 x 102, k = 0.21), and thrips (Re = 1.2 x 101, k = 0.25) in hover. Different representative kinematic param­eters (flapping amplitude, flapping frequency, and type of prescribed actuation) and

Figure 3.62. Hovering Japanese White-eye wake flow fields on a frontal plane. Color contours represent the vorticity distribution of the flow fields. (a-c) Near-wake flow fields pertaining to kinematic phases of the ventral clap; purple patches mark the position of the two wings, and purple dotted lines indicate an outline of the bird. (d) The far-wake flow field beneath a hovering Japanese White-eye after phase 3; thick red arrows depict the trends of the flow motion. (a-d) Thick red arrows show the trends of flow motions. (e) Schematic sketches summarizing the wake flow structures for the three kinematic phases. Black arrows indicate fluid jets; orange and blue spiral arrows represent, respectively, the LEV and TEV. Purple arrows signify the downward jet generated by the downstroking wings executing the ventral clap. From Chang et al. [391].

dimensionless numbers (Reynolds number, reduced frequency) are considered for each insect model [225]. The Reynolds number and reduced frequency are calculated based on mean chord and tip velocity. The morphological and kinematical model of a hawkmoth was already shown in Figure 3.56 and Figure 3.57. For other insect models, similar information and computational models can be obtained in Liu and Aono [225].

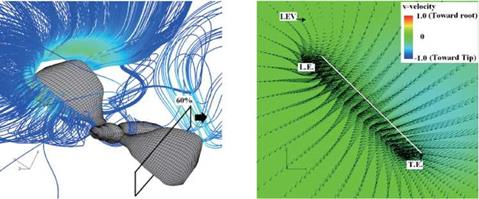
Figure 3.63 shows the velocity vector field on an end-view plane at 60 per­cent semi-span for these four insects. The LEV structure and the spanwise flow in the hawkmoth and the fruit fly cases (see Fig. 3.63A and C) are in good qual­itative agreement with the corresponding experimental results reported in Birch et al. [283]. For the thrips (Re = 1.2 x 101, к = 0.25), the LEV forms upstream of the leading edge, and spanwise flow is weakest among all cases. For the fruit fly (Re = 1.3 x 102, к = 0.21), the LEV structure is smaller than that of the hawkmoth

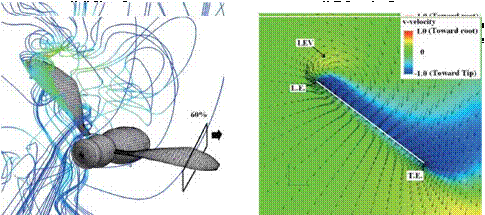and the honeybee. The fruit fly LEV is tube-like and ordered, and spanwise flow is observed around the upper region of the trailing edge. The hawkmoth (Re =

6.3 x 103, к = 0.30) and honeybee (Re = 1.1 x 103, к = 0.24) cases yield much more pronounced spanwise flow inside the LEV and upper surface of the wing, which together with the LEV forms a helical flow structure near the leading edge (see Fig. 3.63A-1 and B-1). Figure 3.64 shows the spanwise pressure gradient contours on the wing of four typical insects at the middle of the downstroke. Compared to the hawkmoth and the honeybee, even though the wing kinematics and the wing-body geometries are different, fruit flies, at a Re of 1.0 x 102~2.5 x 102, cannot create as steep pressure gradients at the vortex core; nevertheless, they seem to be able to maintain a stable LEV during most of the down – and upstroke. Although the LEVs on both the wings of the hawkmoth and honeybee experience a breakdown near the middle of the downstroke, the LEV on the fruit fly’s wing remains attached during

the entire stroke, eventually breaking down during the subsequent supination or pronation [387].

In reality the thrips wings are extremely small – of the order of 1 mm – and are composed of a comblike planform with solidity ratios of 0.2 and less [398]. Consequently, the Reynolds numbers are so low that the viscous effects dominate and the unsteady viscous flow around their wings can be approximated as Stokes flow. Using slender-body theories the flow physics around an array of oscillating bodies was studied by Weihs and Barta [398] and Barta [399]. They showed that the comblike wings of thrips are able to produce forces similar to those of solid wings, while being able to save weight.