Stereo PIV

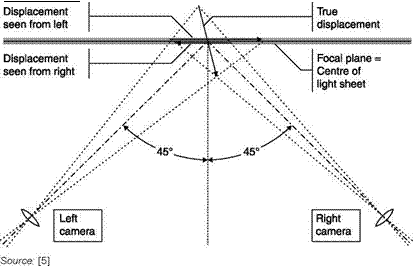
The 3D PIV uses the stereoscopic principle to identify the three components of speed in a flat section of the flow field determined by the laser light sheet. The 3D (Dx, Dy, Dz) displacement is estimated by a couple of 2D (Dx, Dy) displacements as seen by the left and right cameras (Figure 4.35). The greater the angle between the two cameras, the more accurate is the determination of the displacement Dz.

The 3D processing requires a numerical model that describes how objects in space are seen by the CCD camera. The parameters of the numerical model are obtained from a preliminary calibration of the

camera framing markers whose position is known: it serves to identify a common coordinate system for the two cameras.

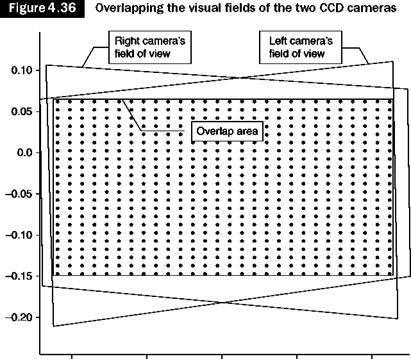
Obviously, the 3D assessment is only possible within the area covered by both cameras. (Figure 4.36). Because of the perspective distortion, each camera covers a region of the trapezoidal plate light. Careful alignment to maximize the overlap area is required.

The stereoscopic measurement begins by processing the simultaneous images produced by two cameras. Two 2D vector maps are obtained that describe the flow field as seen by each of the two cameras. Using the calibration function with the parameters obtained during calibration of the camera, the points of the interrogation grid are reported from the plane of the light sheet on the left and right image planes (planes of the CCDs). With the 2D displacement seen by both cameras and estimated at the same point of the physical space, the 3D displacement of the particle can be calculated by solving the equations obtained in calibration.

When the light sheet is observed at an angle different from 90°, the image plane of the camera, the plane of the CCD, must be rotated as required to properly focus the entire field of view of the camera. The planes of the image, of the lens and of the object must intersect along a common line in order to obtain a properly focused image. This is called the Scheimpflug condition.