AERODYNAMIC SHAPE OPTIMIZATION METHODS

G. S. Dulikravich

The Pennsylvania Stale University, University Park, PA. USA

11.1 Introduction

Although fast and accurate in creating aerodynamic shapes compatible with the specified surface pressure distribution, the inverse shape design methods create configurations that arc not optimal even at the design operating conditions [ 163). 1164] At off design conditions, these configura­tions often perform quite poorly except w hen the specified surface pressure distribution, if avail­able at ail. would be provided by an extremely accomplished acrodynamicist. When using inverse shape design methods, it is physically unrealistic to generate a 3-D aerodynamic config­uration that simultaneously satisfies the specified surface distribution of flow variables, manu­facturing constraints (smooth variation of a lifting surface sweep and twist angles, smooth variation of its taper, etc.) and achieves the best global aerodynamic performance (overall total pressure loss minimized. Iifl/drag maximized, etc ). The designer should use an adequate global optimization algorithm that can utilize any available flow-field analysis code without changes and efficiently optimize the overall aerodynamic characteristics of the 3-D flight vehicle subject to the finite set of desired constraints. The constraints could be purely geometrical or they can be of the overall aerodynamic nature (minimize overall drag for the given values of flight speed, angle of attack and overall lift force, etc ). These objectives can only be met by performing an aerodynamic shape constrained optimization instead of an inverse shape design.

The size and shape of the mathematical space that contains all the design variables (for example, coordinates of all surface points) is very large and complex in a typical 3-D case. To find a global minimum of such a space requires a sophisticated numerical optimization algo­rithm that avoids local minima, honors the specified constraints and stays within the feasible design domain The design variable space in a typical aerodynamic shape optimization has a

number of local minima. These minima are very hard to escape from even by switching the objective function formulation [165) or consecutive spline fitting and interpolation of the unidi­rectional search step parameter (166).

There are several fundamental concepts in creating an optimization algorithm. One family of optimisation algorithms is based on reducing the objective or cost function (for exam­ple. aerodynamic drag) by evaluating die gradient of the cost function and then updating the design variables in the negative gradient direction (167). Evolution search or genetic algo­rithms is another family of optimization algorithms that is based on a semi-random sampling through the design variable space and docs not require any gradient evaluations [168). |I69|. Since both families of optimization algorithms require flow-field analysis to be performed on every perturbed aerodynamic configuration, the optimization of 3-D aerodynamic shapes is a very computationally intensive task

In a gradient-search optimization approach the flow analysis code must be called at least once for each design variable during each optimization cycle in order to compute the gra­dient of the objective function if one-sided finite differencing is used for the gradient evaluation. If a more appropriate central differencing is used for the gradient evaluation, the number of calls to the 3-D flow-field analysis code will immediately double Despite this, the optimization algorithms arc still often misused to minimize the difference between the specified and the com­puted surface flow data in inverse shape design – a task that is significantly more economical when accomplished w ith any of the standard inverse shape design algorithms.

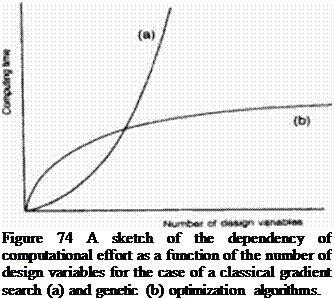The most serious drawback of the brute force application of the gradient search opti­mization in 3-D aerodynamics is that the computing costs increase nonlincarly with the growing number of design variables thus making these algorithms suitable for smaller optimization problems. On the other hand, the computing cost of using evolution search algorithms increases only moderately with the number of design variables (Figure 74) thus making these algorithms more suitable for large optimization problems. Only these optimization algorithms that require minimum number of calls to the flow-field analysis code will be realistic candidates for the 3-D aerodynamic shape optimization

Since the actual 3-D flow-field analysis codes of Euler of Navicr-Stokes type arc very lime consuming, the designer is forced to restrict the design space by working with a relatively small number of the design variables for parameterization (fitting polynomials» of either the 3-D surface geometry (17()|-(172J or the 3-D surface pressure held 1173]. [174]. The optimization code then needs to identify the coefficients in these polynomials. The most plausible choices arc cubic splines. Chebyshev and Fourier polynomials [I75]-(177] are not advisable because they become excessively oscillatory with the increasing number of terms in the polynomial. Moreover, when perturbing any of the coefficients in such a polynomial, the entire 3-D shape will change. Since it is absolutely necessary to constrain and sometimes disallow motion of par­ticular parts of the 3-D surf ace, the most promising choices for the 3-D parameterization appear to be different types of b-splincs 1178], (179), 1171 ]. (180]. local analytical surface patches

[181] . and local polynomial basis functions 1182]. Only when it is possible to use simple and very fast flow-field analysis codes could we afford an ideal optimization situation where each surface grid point on the 3-D optimized configuration is allowed to move independently.

Single-cycle optimization (183] oilers one viable approach at reducing the computing costs. Here, the flow-field analysis code is run on each perturbed aerodynamic configuration for only a small number of iterations (instead to n full convergence» before an optimizer is used to determine the new geometry. An optimal aerodynamic shape is then found by optimally weigh­ing each of the number of feasible configurations that can be obtained using inverse design methods. Hence, this optimization approach guarantees that the final configuration will he real­istically shaped and manufacturable, although the range of geometric parameters to be opti­mized is limited by the geometry’ of the extreme members of the original family of configurations.