Elliptic Loading

For an elliptical load, as shown in Figure 8.4, the (k(y), y) curve is an ellipse. If P is a point on the span whose eccentric angle is в, we have y = —b cos в and therefore:

k(y) = k0 sin в, (8.30)

where k0 is the value of k(y) at y = 0. It is easily seen that the elimination of в gives:

which is an ellipse.

Substituting y = —b cos ф in Equation (8.15), the downwash velocity at the trailing edge is:

Thus for elliptic loading, the downwash velocity is the same at every point on the trailing edge. Now, by substituting Equation (8.28) into Equation (8.29), we get:

where a0′ and a’ refer to the section at distance y from the plane of symmetry.

The chord c’ and incidence a’ depend, in general, on the particular profile section considered, that is on в. Also k0/V depends on the incidence of the aerofoil. If we increase the incidence of the aerofoil by в, the incidence of each profile section will also increase by в. Thus:

2 sin в 1

~—Г + 7

c a.0 b

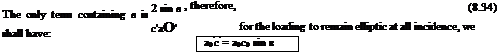where (ki) denotes the new value of Vi. From Equations (8.32) and (8.33), we get:

	2 sin в	1
	c’a0′	b

k0 V

= в.

where c0 is the chord of the middle section of the aerofoil (that is, at y = 0), and a0′ will be same at every section and Equation (8.34) becomes:

c’ = c0 sin в.

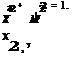This implies that the plot of chord c’ against y is also an ellipse. This situation can be realized by an aerofoil so constructed that its planform is bounded by two half ellipses whose major axis is equal to the span of the aerofoil. This can be proved by using the ellipses:

It follows that:

X1 _ X2 _ X1 ± X2 a1 a2 a1 ± a2

and if C — x1 ± x2, c0 — a1 ± a2, Equation (8.35) is satisfied.

Finally, it is evident from Equations (8.32) and (8.34) that for elliptic loading, which remains elliptic for all incidences, the incidence is the same at every profile section, and k0 is proportional to the incidence, and therefore, from Equation (8.31), the downwash is proportional to the incidence.

Another case arises for an aerofoil of rectangular planform. Here the chord c’ may be taken as constant and equal to c0. Retaining the hypothesis that a0′ — a0, which will be true if the sections are similar, or if they are thin, Equation (8.32) becomes:

This shows that the incidence at each section is different, so that the aerofoil is twisted. The incidence at the middle section will be a, got by assigning в — n/2 in Equation (8.36), and therefore:

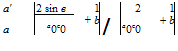(8.37)

Equation (8.37) shows that if the loading is elliptic at the incidence a, it ceases to be elliptic at a different incidence.