Detection of transition

Transition from a laminar to a turbulent boundary layer can be detected by the increases in adiabatic wall temperature and/or film coefficient. These methods are additional to those listed in Chapter 6 (visualization methods, optical methods), to the measurement of stagnation pressure at
a fixed distance from the wall or to the measures of turbulence in the boundary layer with anemometers (Chapters 3 and 4).

5.1.1 Measurement of the temperature recovery factor

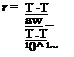The adiabatic wall temperature is usually expressed in a non-dimensional form, temperature recovery factor, r, defined as the ratio between the actual rise in temperature of the adiabatic wall with respect to the static temperature of the stream (Taw – TJ, and the temperature rise that would occur if the flow were stopped isoentropically (T0„ – TJ. The temperature recovery factor can be expressed in terms of the Mach number, the adiabatic wall temperature and the stagnation temperature as follows:

The recovery factor depends only on the Prandtl number, Pr = Cppll where Cp [/Kg-1^-1] is the specific heat at constant pressure. The Prandtl number is a measure of the relative importance of the dissipation of kinetic energy due to the dynamic viscosity, m [Kgm-1s-1], and the heat conduction due to the coefficient of conductivity, l [/K_1m-1s-1]. In the boundary layer the viscous stresses tend to increase the local temperature to a greater extent when the shear rate is strongest (near the wall), the conductivity creates a heat flow toward the colder areas (furthest from the wall) which makes the temperature near the wall to decrease. For gases, which have Pr < 1, the second effect is more important than the first one, therefore the resulting adiabatic wall temperature is lower than the stagnation temperature.

Equations linking the recovery factor to the Prandtl number are different according to the regime of flow, laminar or turbulent. For a flat plate:

r = VPT in the laminar regime,

r = -^PT in the turbulent regime

Because, for air, Pr < 1, the recovery factor is higher in the turbulent than in the laminar flow regime usually passing through a maximum in the region of transition.

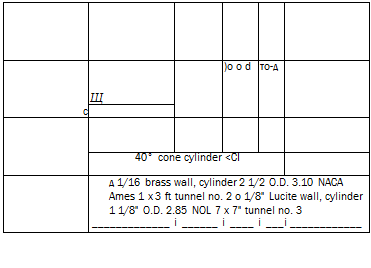
If the transition from laminar to turbulent boundary layer occurs, there are conditions for non-uniform wall temperature on the body and heat flows from the turbulent zone to the laminar zone, leveling out the temperatures (the brass wall in Figure 5.8). In order to measure the true adiabatic wall temperature, care must be taken to minimize the effects of conduction along the wall: the model must therefore be made of an insulating material (the lucite wall in Figure 5.8).

Since the position of the transition, namely the critical Reynolds number, depends also on the intensity of turbulence of the incoming stream, sometimes to determine the quality of a supersonic or hypersonic wind tunnel transition cones are used with apex angles of 5° or 10°. The procedure consists of measuring the critical Reynolds number for the whole range of Mach numbers and Reynolds numbers of the wind tunnel and comparing the data obtained with those of similar wind tunnels. Then it can be decided if additional turbulence screens or other modifications of the wind tunnel are needed.

Figure 5.8

1

о

ф

2

э

25

ф

о.

Е

,ф

Source: [1]

Schematic of the transition cone JPL

Source: [2]

To apply this technique, the cone should have:

■ dimensions such that local Reynolds numbers between 2 x 106 and 7 x 106 can be generated on the surface;

■ low heat capacity;

■ very accurate surface finish.

The cone of Figure 5.9 is hollow and made of fiberglass, except the tip that is made of steel. Thirty copper-constantan thermocouples are arranged on the surface at intervals of 2 cm. The surface is covered with several layers of plastic coating, straightened and painted.

The cone is calibrated in an oven to check that all the thermocouples are working and that their readings are uniform. Once inserted in the wind tunnel and the test has been carried out, the readings of the thermocouples are converted into temperature recovery factor, r, by Equation (5.1). The typical result of a test is shown in Figure 5.10. In the first part of the cone, where the flow is laminar, the temperature recovery factor has a value of about 0.85, in transition a maximum value of about 0.894 is attained and finally it stabilizes at the turbulent value (0.886).

Determination of the critical Reynolds number in a wind tunnel with a transition cone

x(cm)

It should be noted that there is not unanimity in the choice of the characteristic length to be used in calculating the critical Reynolds number. The different methods can lead to variations of l + 2 x 106 in the calculation of Recr.