Surface Green’s Function: Pressure as the Matching Variable

Eqs. (14.1) and (14.2) are linear. The solution of these equations satisfying boundary condition p = pEuler on surface Г can be found by means of a Green’s function. For clarity, a superscript “g” is used to denote the variables of the Green’s function. Let (f, n, s) be a set of body-fitted curvilinear coordinates. The surface Г corresponds to g = g0. The Green’s function (v(g), p{g)) satisfies the following boundary value problem:

d v(g)

Po—~ + V p(g) = 0 (14.8)

dt

+ YPqV ■ v(g) = 0 (14.9)

dt

On Г, i. e., g = Sq,

p(g)(x, t; fo, no, So, to) = S(f – fo)S(n – По)S(t – to) (14.10)

(Note: The notation that the first set of spatial and time argument of the Green’s function represents the location and time of the observer while the second set rep­resents that of the source is adopted here.)

When the Green’s function is found, the far-field pressure is given by

TO

p(x, t) = /// p(g) (X, t; fo, no, g0, t0)pEuler(f0, n0, g0, t0)df0 dn0 dt0• (14.11)

— TO

As an example of the use of surface Green’s function, the case of Г in the form of an infinite circular cylindrical surface of diameter D (see Figure 14.2) is considered. The cylindrical coordinates (r, ф, x) are the natural body-fitted coordinates of this problem. By eliminating v(g) from Eqs. (14.8) and (14.9) in favor of p(g) and upon applying Fourier transform to t, the time variable, the governing equation for p (the Fourier transform of p(g)), is found to be

Figure 14.3. Branch cuts for the square root function (k2

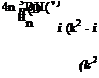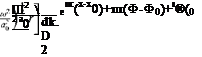The solution of Eq. (14.15) satisfying boundary condition (14.16) can easily be found in terms of Hankel function []. On inverting the Fourier transform in x and the sum over n, it is found that

The branch cuts for the square root function (k2 – 4-) 2 in the k plane is shown

a0

in Figure (14.3).

For radiation to the far field, it is advantageous to switch to polar coordinates (Я, в,ф) (see Figure 14.4) with

x = R cos в, r = R sin в

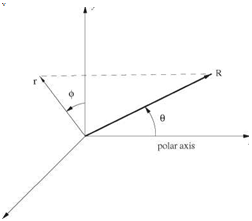Figure 14.4. Spherical polar coordinates (R, в, ф), cylindrical coordinates (г, ф, x), and Cartesian coordinates (x, y, z).

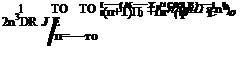For large R, the Hankel function in the numerator of Eq. (14.17) may be replaced by its large argument formula. The к – integral can then be evaluated by the method of stationary phase. Upon inverting the Fourier transform in t, the far field Green’s function is found to be

(14.18)

As a simple demonstration that Eq. (14.18) is the correct surface Green’s func­tion, the case of a sound field produced by a time periodic monopole of angu­lar frequency L located at the origin of coordinates is considered. The pressure field is

where R is the radial distance. On the cylindrical surface of diameter D, the polar dis­tance is R = (D – + x2)1/2 for a point at x = x0. Thus, the fluctuating surface pressure is given by

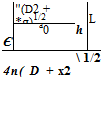
(14.2o)

By inserting p(g) from Eq. (14.18) and p(x0, ф0, t0) from Eq. (14.20) into Eq. (14.11), the far-field pressure due to surface pressure on the cylindrical surface is

+ x2) Ho(1)(fDsm в)

The right side of Eq. (14.21) may be integrated step by step as follows. Inte­gration over dф0 is zero except for n = 0. In this case, the integral is 2n. Integra­tion over dt0 gives 2nS(m — L). Therefore, on integrating over dm, the right side simplifies to

Now, from the extensive compilation of Fourier integrals of Erdelyi et al (1954), the following closed-form integral is found:

n eib(x2+a2)1/2—iyx

f (x2 + a2)1/2 dX = ІПH0(1) [a(b2 – У2)1/2] •

—r

By means of Eq. (14.23), it is straightforward to simplify Eq. (14.22) to

Thus, the monopole sound field at large R is recovered.