Computation of the Adjoint Green’s Function: Free Field Solution
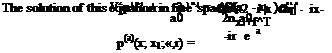 |
|
By eliminating v(a) from Eqs. (14.49) and (14.50), the governing equation for p(a) is found to be
Let (Я, в,ф) be the coordinates of a spherical polar coordinates system with the x-axis as the polar axis (see Figure 14.4). Also, let (r, ф, x) be the coordinates of a cylindrical coordinate system with the x-axis as its axis. For convenience, the source vector x1 is taken to lie on the plane ф = ф1, then
x1 = R1 cos 01ex + R1 sin в1 cos ф1ёv + R1 sin в1 sin ф1ё z. Also, the position vector x is
x = x ёх + r cos ф ё v + r sin ф ё_.
![]()
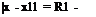 For large R1 (R1 ^ to), the distance between x1 and x is |x ■ x1|
For large R1 (R1 ^ to), the distance between x1 and x is |x ■ x1|
|x1l
Thus, Eq. (14.54) may be rewritten as
where e0 = 1, em = 2 for m > 1. The first line of Eq. (14.55) is just the plane wave solution for a source at a great distance. This is illustrated in Figure 14.7. The second line of Eq. (14.55) is the cylindrical wave expansion (see chapter IX of Magnus and Oberhettinger, 1949). Eq. (14.55) is only a part of the adjoint Green’s function. The second part is the scattered wave. It will be shown that the scattered wave part of the adjoint Green’s function may be computed as a two-dimensional problem.













