Isentropic Flow

Our heavyweight helicopter equal in the world does not have

In Rostov started production of the most load-lifting rotary-wing car The Russian holding «Helicopt[...]

The old plane — nonsense, pilots think - there was an attack

In spite of the fact that the main version of crash of the Russian plane of the Kogalymavia company [...]

The fundamental equations for isentropic flows can be derived by considering a simplified model of a one-dimensional flow field, as follows.

Consider a streamtube differential in equilibrium in a one-dimensional flow field, as represented by the shaded area in Figure 9.1. p is the pressure acting at the left face of the streamtube and (p + ||ds) is the pressure at the right face. Therefore, the pressure force in positive s-direction, Fp, is given by:

dp dp

Fp = p dA — p + ds dA = — ds dA.

ds ds

For equilibrium, dm (dV/dt) = sum of all the forces acting on the streamtube differential, where dm is the mass of fluid in the streamtube element considered, and dV/dt is the substantial acceleration.

	dV	dV
dV =	dt +	ds
	dt	ds
dV	dV dt	dV ds
— =	— — +	— —
dt	dt dt	ds dt

In the above equation for substantial acceleration, dV/dt is the local acceleration or acceleration at a point,

dV ds dV

that is, change of velocity at a fixed point in space with time. The convective acceleration——– = V —

ds dt ds

is the acceleration between two points in space, that is, change of velocity at a fixed time with space. It is present even in a steady flow.

The substantial derivative is expressed as:

dV dV dV

= + V.

dt dt ds

Therefore, the equilibrium equation becomes:

dp dV

— ds dA = dm. ds dt

But dm = p dA ds. Substituting this into the above equation, we get:

dV _ 1 dp

dt p ds

that is:

Equation (9.13) is applicable for both compressible and incompressible flows; the only difference comes in solution. For steady flow, Equation (9.13) becomes:

Подпись: (9.14) dV 1 dp
V— + – — = 0.

ds p ds

Integration of Equation (9.14) yields:

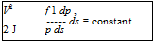Подпись: (9.15)

This equation is often called the compressible form of Bernoulli’s equation for inviscid flows. If p is expressible as a function of p only, that is, p = p(p), the second expression is integrable. Fluids having these characteristics, namely the density is a function of pressure only, are called barotropic fluids. For isentropic flow process:

p _	constant	(9.16)
pY =	/ 1/Y

p2 _ I	El	(9.17)
p1 ‘	kpJ ’

where subscripts 1 and 2 refer to two different states. Therefore, integrating dp/p between pressure limits p1 and p2 , we get:

Using Equation (9.18), Bernoulli’s equation can be written as:

Equation (9.19) is a form of energy equation for isentropic flow process of gases.
For an adiabatic flow of perfect gases, the energy equation can be written as:

(9.20a)

y P2 v[ = y pi

Y – 1 P2 2 y – 1 Pi 2

Y P + V2 _ Y P0 Y – 1 P 2 y – 1 Po

(9.20c)

Equations (9.20) are more general in nature than Equation (9.19), the restrictions on Equation (9.19) are more severe than those of Equation (9.20).

Equations (9.20) can be applied to shock, but not Equation (9.19), as the flow across the shock is non-isentropic. With Laplace equation a2 = YP/P, Equation (9.20c) can be written as:

V2 a2 _ Y P0

2 Y – 1 Y – 1 P0

(9.20d)

V2 a2 a0

—— 1———- = ——.

2 y – 1 Y – 1

(9.20e)

The subscript “0” refers to stagnation condition when the flow is brought to rest isentropically or when the flow is connected to a large reservoir. All these relations are valid only for perfect gas.