A Test Case: A Broadband Monopole Source

To provide a simple validation test for formula (14.102), reconsider the case of the monopole noise source problem discussed in section 14.5.2 (see Figure 14.12). Instead of a time periodic source, it is replaced by the broadband monopole source of Section 14.6. The half-apex angle of the conical surface 5 is again taken to be 10°. In this case, if Yr is a point on the conical surface, then

Y’ = (R’2 + x2 – 2R’xc cos 5)2.

The two-point space-time correlation function has the following form (see Eq. (14.91)):

Ф(ІЇ, R", &,X) = F

The F-function as computed directly is shown in Figure 14.19. In this special case, Ф is independent of ©. For this reason, the integral over d& in Eq. (14.102) is zero except for n = 0. Thus the far-field noise spectrum obtained by continuation of the pressure field on the conical surface is as follows: [16]

A change of integration variable from X to n = (Y" – Yr – a0X)/D transforms the triple integrals in Eq. (14.103) into three separate integrals. This yields

s (Яв, ф,ю) D

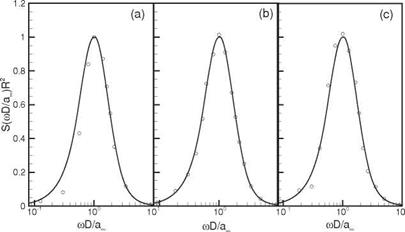
Figure 14.21 shows a comparison of the far-field noise spectra at в = 150°, 90°, and 30° (exhaust angle) computed numerically according to Eq. (14.104) and the original noise spectrum of the broadband monopole source (the similarity spectrum of the noise of large turbulence structures of high-speed jets). The agreement is excellent. The excellent agreement provides strong support for the validity of the present continuation method.

EXERCISE