A Foil with a Jet Flap in Proximity to the Ground
|
= /(*), |
Note that the quadruplication procedure can be applied in all cases when the kernel of the integral equation has a form similar to (10.2). For a foil with a jet flap near the ground, the corresponding integral equation can be written as (see Menshikov [165])
|
/(*) |
where
7 is the strength of the vorticity that replaces the foil and the jet; dy^/dx is the unknown distribution of slope of the jet. The vorticity (pressure difference) on the jet is assumed proportional to the jet momentum coefficient, and the curvature of the jet
1 1 d2?v-
= = x <0. (10.13)
In these relationships, y-,y” represent the local slope and the curvature of the jet and Cj is the jet momentum coeffcicient. Quadruplicating the integral operator, we obtain the following differential equations for the vorticity distributions on the foil and the jet, as well as for the jet camber line:
hp – = 0, 0 < x < 1, (Ю.14)
ax
= = x <0. (Ю.15)
dx 2 dx3 dx
Because the jet is blown from a slot at the trailing edge at a small angle r with
p – (0) = r, p(-oo)=0. (10.16)
dx dx
Accounting for (10.16), it is easy to derive the solution in the form
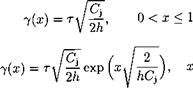 (10.17)
(10.17)
(10.18)
The corresponding lowest order lift coefficient is given by
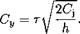 (10.19)
(10.19)
This expression is identical to that obtained within the boundary problem formulation for a jet-flapped wing in the ground effect; see formula (6.123).











