Application to Bodies of Revolution and Fuselage

The general, three-dimensional equations can be applied to these shapes. But it is more convenient to use polar coordinates for bodies of revolution and fuselage.

The potential equation in cylindrical polar coordinates, for incompressible flow is:

д2ф д2ф і дф і д2ф

дx2 + dr2 + r dr + r2 дв2

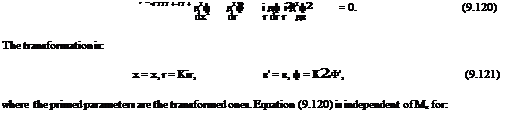
where x, r and в are the axial, radial and angular (circumferential) coordinates, respectively. For com­pressible flow, the equation is:

K1 = |1 – m2I.

From the streamline analogy:

1

1 M2

Here again, as in Cartesian coordinates, transform the geometry and then calculate the aerodynamic coefficients for incompressible case and then the values for compressible case are given by Equation

(9.115). If f = 0, the only transformation required will be t/t = 1 / j 1 — M2 |. The variations of —^,

* HX

—^ j and l-mx / PfnoF with Mx are shown in Figures 9.16(a)-9.16(c), respectively.

da J c^=0 Ex V Ex / inc

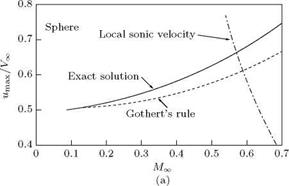
In Figure 9.16(a), it is seen that beyond the chain line the results cannot be applied because once the speed of sound is reached locally, there will be shock somewhere and this is certainly a nonlinear effect. Though the plot is for a sphere, which is not a slender body, the results of Gothert rule are quite good (at Mx = 0.5, the error is only ~ 5%). For slender bodies, Gothert’s rule applies very well.

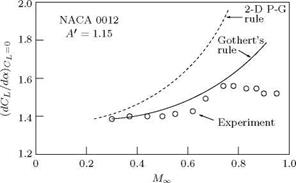
In Figure 9.16(b), the results for NACA 0012 profile with Aspect Ratio (A’) 1.15 are shown. For those Mach numbers for which locally speed of sound is not reached anywhere on the profile, Gothert’s rule agrees very well with experimental values. The Prandtl-Glauert rule for A = x shows that for large A’, the dCL/da obtained is much higher.

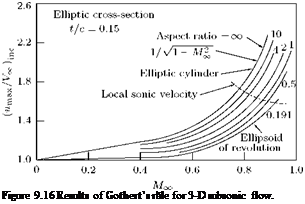
The three-dimensional relief effect is shown in Figure 9.16(c). For an infinitely long circular cylinder in a stream of velocity Ex, Mmax = Ух, but for a sphere Mmax = 0.5Ex. From the plot, the 3-D relief effect increases with increase in Mx. A slender body (small A’) introduces smaller perturbations, that is, the disturbances produced by wings are much more as compared to fuselage. This difference in disturbances

(b)

of wings and fuselage is greater at larger Mx. So, locally, speed of sound is reached first on wings and not on fuselage. That is, we should find out the critical Mach number for wings and not for the fuselage, since only the former is significant. The critical Mach number Mcr for the fuselage will be much higher than the Mcr for the wing.

Comparison of Two-Dimensional Symmetric Body and Axially Symmetric Body

For an axisymmetric body, in any cross-section the flow will be same. But this will not be so for a two­dimensional body. Also, at any cross-section, the disturbances produced by an axisymmetric body will be much smaller, that is, the acceleration of flow will be much less and hence the drop in the pressure coefficient Cp is much smaller compared to a two-dimensional body.