Special Case of Hover
In hovering flight the uncoupled longitudinal and lateral motions break down further. Longitudinal motion resolves into an uncoupled vertical velocity mode and an oscillatory mode coupling forward velocity and pitch attitude. In a similar manner, lateral motion breaks down into an uncoupled yaw mode and an oscillatory mode coupling lateral velocity and roll attitude. Both of these coupled modes are dynamically unstable. The physical nature of the longitudinal oscillation is illustrated in Figure 8.5 and can be described as follows.
|
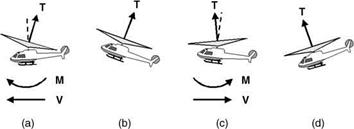
Figure 8.5 Longitudinal dynamic instability in hover |
Suppose the hovering helicopter was to experience a small forward velocity as at (a). This would usually be the effect of a small horizontal gust impinging on the aircraft. Incremental flapping creates a nose-up disc tilt, which results in a nose-up pitching moment on the aircraft. This is as described in Section 8.3.2 (the important overall qualification being that there is no significant aircraft drag force). A nose-up attitude develops and the backward – inclined thrust opposes the forward motion and eventually arrests it, as at (b). The disc tilt relative to the rotor shaft and hence the rotor moment have now been reduced to zero. A backward swing commences, in which the disc tilts forward, exerting a nose-down moment, as at (c). A nose-down attitude develops and the backward movement is ultimately arrested, as at (d). The helicopter then accelerates forward under the influence of the forward inclination of thrust and returns to the situation at (a). Mathematical analysis shows, and experience confirms, that the motion is dynamically unstable, the amplitude increasing steadily if the aircraft is left to itself.
This longitudinal divergent mode and its lateral-directional counterpart constitute a fundamental problem of hovering dynamics. They require constant attention by the pilot, though since both are usually of low frequency, some degree of instability can generally be allowed. It remains the situation, however, that ‘hands-off’ hovering is not possible unless a helicopter is provided with an appropriate degree of artificial stability.