Axially symmetric fields
Assume that the field is symmetrical about the x axis and that the direction of observation is z (Figure 6.46). The local value of the refractive index becomes a function of x and r = ^y2 + Z where r is the distance from the axis of symmetry.
Assuming that the rays of light go through the test section along the z direction, as in the case of Figure 6.46, if there is no refraction on the edge of test section, i. e. if n(rj = n0, the problem can be solved transforming Equations (6.10) (6.15) and (6.16) in the axially symmetric coordinate system:
In the Schlieren system:
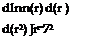
![]()
![Подпись: Source: [4]](/img/3131/image398_0.gif) |
C(y) = f y a
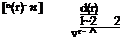 |
||
In the separated-beams interferometer:
In the differential interferometer:
![]() Ml = Jr r dn(r) dr1
Ml = Jr r dn(r) dr1
7 J r=y dr r-yy
The integration is performed starting from the y coordinate of the ray in question until the outer radius, rm enclosing the axisymmetric field is reached. It is assumed that the index of refraction is nm = n0 = const for r > rm, i. e. outside the test field.
Equations (6.36), (6.37) and (6.38) are integral equations of the Abel type. The quantity to be determined, n or dn/dr, must be calculated from inside the integral. In principle, there are two ways to solve this problem. The first way is analytic (Abel inversion). The solution can be obtained by applying to both sides once again the operator
![]() d(y)
d(y)
l~2 2
Vr – y
and reversing the order of integration in the double integral created at the second member. For example, in the case of separated-beams interferometer, Equation (6.37), the Abel inversion provides:
The integration should be done on the measured function Ml (y), difference of the optical paths. Since this is available as a set of discrete values, these values should be fitted with an appropriate analytic function. A disadvantage of this approach is the further differentiation of the function needed in Equation (6.39).
Applying the Abel inversion to Equations (6.36) and (6.38), is obtained directly:
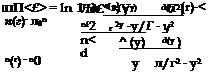 |
In the first member of Equation (6.38), the approximation was made:
Surprisingly the results for the differential interferometer, Equation (6.41), and the Schlieren system, Equation (6.40), are less complicated than that for the separated-beams interferometer, Equation (6.39), because the index of refraction can be achieved without the need for additional differentiation of the function approximating the experimental data.
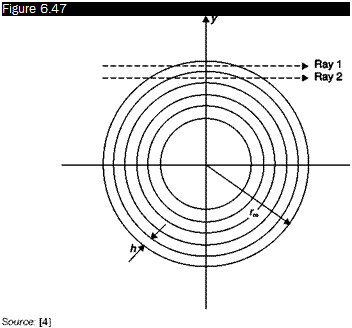 |
Subdivision of the axially symmetric field in annular zones with thickness h
The second method for solving the axially-symmetric problem prevents the use of the Abel inversion through a numerical procedure. To this end, the cross-section of the axially-symmetric field is divided in rings of radius r (Figure 6.47). The amount to be determined is a supposed constant in each zone. The procedure is a step-by-step solution that starts from the outer edge rM of the field and can be easily computed.













