Application of Thin Aerofoil Theory

Applying the thin aerofoil theory relation, Equation (9.184), for the flat plate shown in Figure 9.34(c) at a small angle of attack a0, the Cp on the upper and lower surfaces of the plate can be expressed as:

Cp = ^—ta=. (9.185)

vM – 1

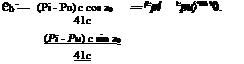where the minus sign is for Cp on the upper surface and the plus sign is for Cp on the lower surface. The lift and drag coefficients are respectively given by:

In the above expressions for CL and CD, cos a0 ^ 1 and sin a0 ^ a0, since a0 is small and the subscripts i and u refer to the lower and upper surfaces, respectively and c is the chord. Therefore:

Cl — (Cpi – Cpu)

CD — (C pi Cpu)a0.

Using Equation (9.185), the CL and CD of the flat plate at a small angle of attack may be expressed as:

(9.186)

Now, consider the diamond section aerofoil shown in Figure 9.34(a), with nose angle 2s, at zero angle of attack. The pressure coefficient Cp on Two-Dimensional Compressible Flows

The equations of motion in terms of velocity potential for steady, irrotational isentropic motion, as derived in Section 9.7, turn out to be nonlinear partial differential equations. Although the equations were derived somewhat easily, exact solutions of these equations for particular flow problems often involve tedious mathematical procedures; in many cases, solutions are not possible. To solve this problem, the following two courses of action seem to be open:

. Find exact solutions for a simplified problem with the hope of obtaining a qualitative understanding of the nature of other flow patterns for which solutions are not available.

2. Find simple, though approximate, solutions suitable for practical applications. Both methods of ap­proach yield useful information and in a sense complement each other, as the few exact solutions serve as a check to the validity and reliability of the approximate methods. In this chapter, we shall see how the second method may be applied to some important problems of two-dimensional flow.

The assumption of two-dimensionality itself serves as a first approximation to the flow past the wings of airplane, the flow through the blade system of propellers and of axial-flow in compressors and turbines. In many such applications the velocity of perturbations produced by the body immersed in the flow are small, because the bodies are very thin. In this fact lies the essence of the linearized method – that the flow pattern may be thought of as the combination of a uniform, parallel velocity on which small perturbation velocities superposed.

The advantage of making such an assumption lies in the fact that the governing equation of motion is greatly simplified and also becomes linear. Further, it is shown that, from this linearized theory or small perturbation theory, we can draw useful approximate information as to the effect of Mach number for subsonic flow. The linearized theory also makes evident, an approximate similarity law for different flow fields.