Visual perception in flight control – optical flow and motion parallax

One of the earliest published works on visual perception in flight control presented a mathematical analysis of ‘motion perspective’ as used by pilots when landing aircraft (Ref. 8.11). The first author of this work, James Gibson, introduced the concept of the optical flow and the centre of expansion when considering locomotion relative to, and particularly approaching, a surface. Gibson suggested that the ‘psychology of aircraft landing does not consist of the classical problems of space perception and the cues to depth’. In making this suggestion, Gibson was challenging conventional wisdom that piloting ability was determined by the sufficiency of linear/aerial perspective and parallax cues. Gibson had earlier introduced the concept of motion perspective in Ref. 8.12, but in applying it to flight control he laid the foundation for a new understanding of, what we might generally call, spatial awareness. To quote from Ref. 8.11:

Speaking in terms of visual sensations, there might be said to exist two distinct characteristics of flow in the visual field, one being the gradients of ‘amount’ of flow and the other being the radial patterns of ‘directions’ of flow. The former may be considered a cue for the perception ofdistance and the latter a cue for the perception of direction of locomotion relative to the surface.

Gibson focused mainly on fixed-wing landings but he also presented an example of the optical flow-field generated by motion perspective for the case of a helicopter landing vertically, as shown in Fig. 8.3. ‘For the case of a helicopter landing, the apparent

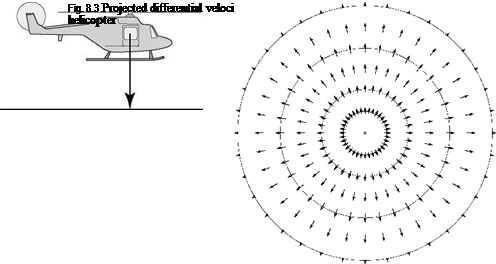
velocity of points in the plane below first increases to a maximum and then decreases again.’ The optical flow-field concept clearly has relevance to a helicopter landing at a heliport, on a moving deck or in a clearing, and raises questions as to how pilots reconstruct a sufficiently coherent motion picture from within the confines of a closed – in cockpit to allow efficient use of such cues.

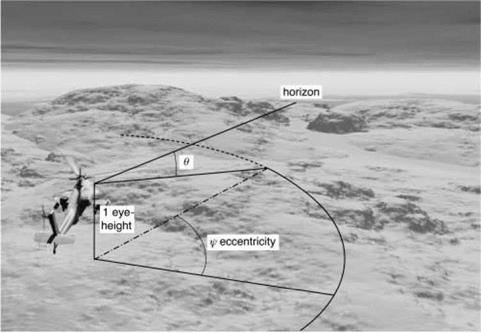
Gibson’s ecological approach (Ref. 8.13) is a ‘direct’ theory of visual perception, in contrast with the ‘indirect’ theories which deal more with the reconstruction and organization of components in the visual scene by the visual system and associated mental processes (Ref. 8.14). The direct theory can be related to the engineering theory of handling qualities. The flight variables of interest when flying close to obstacles and the surface are encapsulated in the definition of performance requirements in the ADS – 33 flight manoeuvres – speed, heading, height above surface, flight path accuracies, etc. In visual perception parlance these have been described as ego-motion attributes (Ref. 8.14) and key questions concern the relationship between these and the optical variables, like Gibson’s motion perspective. If the relationships are not one-to-one then there is a risk of uncertainty when controlling the ego motion. Also, are the relationships consistent and hence predictable? The framework for the discussion is a set of three optical variables considered critical to recovering a safe UCE for helicopter nap-of-the – earth (NoE) flight – optical flow, differential motion parallax and the temporal variable tau, the time to contact or close a gap.

Figure 8.4, from Ref. 8.15 (contained within Ref. 8.16), illustrates the optical flow-field when flying over a surface at 3 eye-heights per second (corresponds to fast NoE flight – about 50 knots at 30-ft height – or the flow-field observed by a running person). The eye-height scale has been used in human sciences because of its value to deriving body-scaled information about the environment during motion. Each flow vector represents the angular change of a point on the ground during a 0.25-s snapshot. Inter-point distance is 1 eye-height. The scene is shown for a limited field-of-view

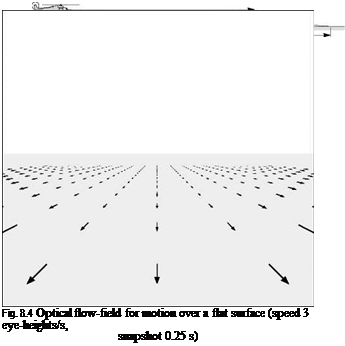window, typical of current helmet-mounted display formats. A 360° perspective would show flow vectors curving around the sides and to the rear of the aircraft (see Gibson, Ref. 8.12). The centre of optical expansion is on the horizon, although the flow vectors are shown to ‘disappear’ well before that, to indicate the consequent ‘disappearance’ of motion information to an observer with normal eyesight. If the pilot were to descend, the centre of optical expansion would move closer to the aircraft, in theory giving the pilot a cue that his or her flight trajectory has changed.

The length of the flow vectors gives an indication of the motion cues available to a pilot; they appear to decrease rapidly with distance. In the figure, the ‘flow’ is shown to disappear after 16 eye-heights.

The velocity in eye-heights per second is given by

In terms of the optical flow, or rate of change of elevation angle 9 (Fig. 8.5), we can write

d9 X. e

dt 1 + x2

where xe is the pilot’s viewpoint distance ahead of the aircraft scaled in eye-heights.

Fig. 8.5 Viewing eccentricity and elevation angles

When the eye-height velocity, xe, is constant, then the optical flow is also constant; they are in effect measures of the same quantity. However, the simple linear relationship between xe and ground speed given by eqn 8.2 is disrupted by changes in altitude. If the pilot descends while keeping forward speed constant, xe increases; if he climbs, xe decreases. A similar effect is brought about by changes in surface layout, e. g., if the ground ahead of the aircraft rises or falls away. Generalizing eqn 8.2 to the case where the aircraft has a climb or descent rate (djz) relative to the ground, we obtain

The relationship between optical flow rate and the motion variables is no longer straight­forward. Flow rate and ground speed are uniquely linked only when flying at constant altitude.

A related optical variable comes in the form of a discrete version of that given by eqn 8.2 and occurs when optically specified edges within the surface texture pass some reference in the pilot’s field of vision, e. g., the cockpit frame usually serves as such a reference. This optical edge rate is defined as

Fig. 8.6 Angular velocity versus distance along ground plane (Ref. 8.15)

optical flow rate, edge rate is invariant as altitude changes. However, when ground speed is constant, edge rate increases as the edges in the ground texture become denser, and decreases as they becomes sparser.

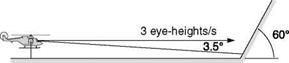
From eqn 8.2, it can be seen that flow rate falls off as the square of the distance from the observer. Figure 8.6, from Ref. 8.15, shows how the velocity, in minutes-of – arc/second, varies with distance for an eye-point moving at 3 eye-heights/s.

Perrone suggests that a realistic value for the threshold of velocity perception in complex situations would be about 40 min arc/s. In Fig. 8.6, this corresponds to information being subthreshold at about 15-16 eye-heights distant from the observer. To quote from Ref. 8.15, ‘This is the length of the “headlight beam” defined by motion information alone. At a speed of 3 eye-heights/sec, this only gives about 5 seconds to respond to features on the ground that are revealed by the motion process’. The value of optical streaming for the detection and control of speed and altitude has been discussed in a series of papers by Johnson and co-workers (Refs 8.16-8.20). Flow rate and texture/edge rate are identified as primary cues. These velocity cues can be picked up from both foveal (information detected by the central retinal fovea) and ambient (information detected by the peripheral retina) vision. An issue with ambient information, however, is the significant degradation in visual acuity as a function of eccentricity. The fovea of the human eye, where there is a massive concentration of visual sensors, has a field of regard of less than 1° (approximately a thumb’s width at arm’s length). The visual acuity at 20° eccentricity is about 15% as good as the fovea for resolution, although Cutting points out that this increases to 30% for motion detection (Ref. 8.21). Cutting also observes that the product of motion sensitivity and motion flow (magnitude of flow vectors) when moving over a surface is such that ‘the thresholds for detecting motion resulting from linear movement over a plane are roughly the same across a horizontal meridian of the retina’.

In Fig. 8.4, the centre of optical expansion or outflow is on the horizon. If the pilot is looking directly at this point then the information seen will be ‘filtered’ by the

0 10 20 30 40 50

Degrees eccentricity ip

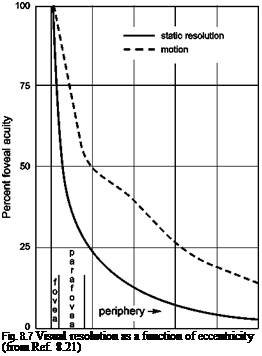
variable sensitivity across the retina. The motion acuity gradient or visual resolution takes the form illustrated in Fig. 8.7 (Ref. 8.21), based on the eccentricity and elevation angles defined in Fig. 8.5.

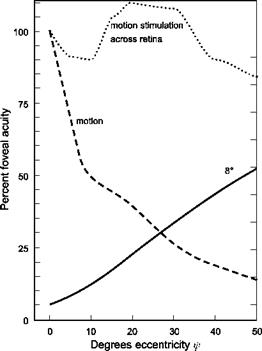
In Fig. 8.7, data are shown for static resolution and motion resolution referenced to the fovea performance of 100. The results show that the strength of visual inputs 20° off-centre reduce to about 40% of those picked up by the fovea when in motion compared with 15% statically. However, the magnitude of the motion flow vectors depicted in Fig. 8.4 increases away from the line of sight in a normalized manner shown in Fig. 8.8 (also from Ref. 8.21). The sensitivity of the retina to motion is therefore the resultant product of the two effects and is actually fairly uniform across a horizontal meridian. Figure 8.9 shows the case for viewing at 8° below the horizon, corresponding to about 7 eye-heights ahead of the aircraft.

A more irregular surface will give rise to deformations in the sensitivity but the same underlying effect will be present, leading to the conjecture that the pilot’s gaze will naturally be drawn to the direction of flight, i. e., that direction which, on average, gives uniform stimulation across the retina. This is good news for pilots, and a determining factor on piloting skill is how well this capability is ‘programmed’ into an individual’s perceptual system.

The subject of way-finding, or establishing the direction of flight, has also been addressed in some detail in Ref. 8.21, where the notion of directed perception was introduced. Cutting developed the optical flow-field concept, arguing that people and animals make more use of the retinal flow-field, fixating with the fovea on specific

Fig. 8.8 Normalized flow vectors as a function of eccentricity (from Ref. 8.21)

0 20 40 60 80

Degrees eccentricity f

Fig. 8.9 Resultant motion threshold function across the retina

Distant objects move more

Fig. 8.10 Differential motion parallax as an optical invariant to aid way finding (from Ref. 8.21)

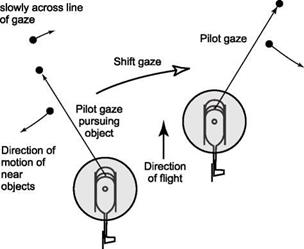
parts of the environment and deriving information from the way in which surrounding features move relative to that point on the retina. In this way the concept of differential motion parallax (DMP) was hypothesized as the principal optical variable used for way­finding in a cluttered environment. Figure 8.10 illustrates how motion and direction of motion can be derived from DMP. The helicopter is being flown through a cluttered environment. The pilot fixates his or her gaze on one of the obstacles (to the left of motion heading) and observes the motion parallax effects on objects closer and farther away. Objects farther away move to the right and those closer move to the left of the gaze (as seen on the retinal array). The pilot can judge which objects are closer and further away by the relative velocities. Figure 8.10 indicates that closer objects move more quickly across the line of gaze. There is no requirement to know the actual size or distance of any of the objects in the clutter. The pilot can judge from this motion perception that the direction of motion is to the right of the fixated point. He or she can now fixate on a different object. If objects further away (slower movements) move
to the left and those closer (faster movements) move to the right, then the pilot will perceive that motion is to the left of the fixated object. By applying a series of such fixations the pilot will be able to keep updating his or her information about direction of motion, and home in on the true direction with potentially great accuracy (the point where there is no flow across the line of gaze). Cutting observed that in high – performance situations, for example, deck landings of fixed – and rotary-wing aircraft, required heading accuracies might need to be 0.5° or better. DMP does not always work however, e. g., in the direction of motion itself or in the far field, where there is no DMP, or in the near field, where DMP will fail if there are no objects nearer than half the distance to the point of gaze (Ref. 8.21).

In Ref. 8.15, Perrone also discusses the question of how pilots might infer surface layout, or the slants of surfaces, ahead of the aircraft. This is particularly relevant to flight in a DVE where controlled flight into terrain is a major hazard and still all too common. The correct perception of slope is critical for achieving ‘desired’ height safety margins for flight over undulating terrain, and hence for providing good visual cue ratings for vertical translational rate, for example. Figure 8.11 illustrates the flow- field when approaching a 60° slope hill about 8 eye-heights away. The centre of optical

Fig. 8.11 Optical flow-field approaching a 60° slope (from Ref. 8.15)

expansion has now moved up the slope and the motion cues over a significant area around this are very sparse. If the pilot wants to maintain gaze at a point where the motion threshold cuts in (e. g., 5 s ahead) he or she will have to lift his or her gaze, and pilots will tend to do this as they approach a hill. This aspect is discussed again later in this chapter when results are presented from simulation research into terrain flight, where the question – how long do pilots look forward? – is addressed.

Any vision augmentation system that tries to infer slope based on flow vectors around the centre of expansion is likely be fairly ineffective. In Ref. 8.22, a novel vision augmentation system was proposed for aiding flight over featureless terrain at night. An obstacle detector system was evaluated in simulation, consisting of a set of cueing lights, each with a different look-ahead time, presenting a cluster of spots to the pilot of the light beams on the terrain ahead of the aircraft. As altitude or the terrain layout ahead changed, so the cluster changed shape, providing the pilot with an ‘intuitive spatial motion cue’ to climb or descend.

In a cluttered environment, the optical variables – flow/edge rate and DMP – appear to provide primary cues to pilots for judging the direction in which they are heading. The question as to how they judge their speed and distance takes us onto the third optical flow variable in this discussion, the results of which suggest that pilots do not actually need to know speed and distance for safe flight control; rather the prospective control is temporally based within an ordered spatial environment.