Evaluation of Speed of Flutter of a Foil Close to the Ground

Herein, the definition of a flutter will be restricted to that of a phenomenon of oscillatory instability of an elastic wing in a potential flow without separation or shock waves. The essential feature of flutter is a certain interaction of the degrees of freedom of an elastic wing, entailing the influx of flow energy to this wing.

In a simple mathematical model of the flutter of a wing in the extreme ground effect, the analysis will focus on the interaction of two degrees of freedom related to elastic heave and pitch oscillations in a two-dimensional flow past a flat plate. To evaluate the speed of flutter, we write equations of the free elastic oscillations of foil in nondimensional form as

fi(h + кЩ – Су – цв(хе – xcg),	(12.2)
/і Іе(0 Ч – &$$) = Tflz ^/l(Xe *Ecg)?	(12.3)

where p = 2M/pSC0 = 2M/pCq • 1 represents the density of the ’’vehicle”, ге = іK; ie is the moment of inertia of mass calculated with respect to the elastic axis, i. e., the point whose abscissa x = xe; xcg is the abscissa of the center of gravity, and kh = u>hC0/U0 and ke = w>eC0/U0 are Strouhal numbers, based on circular frequencies and associated with heave and pitch springs, which model two elastic degrees of freedom of the foil. Representing pitch and heave motions as harmonic oscillations,

6{t) = 0O exp(ikt), h(t) = h0 exp(ikt), (12.4)

where к = ujC0/U0 is the Strouhal number based on circular frequency и of oscillations and і = л/-Л, we can find the lift and the moment (around the abscissa xe of the elastic axis) coefficients Cy and mz by using solutions of the corresponding problems presented in paragraph 3.5. Heave-related coefficients were determined in the following form:

Cyh(t) = j-Ahexp(ikt), Ah = – 4k, (12.5)

m*h = exp(ikt), Bh = B£ – Ahxe, = fc(5fc 8г), (12.6)

where h is the relative ground clearance, measured from the trailing edge of the foil.

The lift and the moment coefficients for pitch oscillations can be found by the following formulas:

)*-xt

г2 г3 у 2 *^е

where

Substituting the expressions for 6(t) and h(t), as well as the heave and pitch contributions to the lift and moment coefficients, we can write the following system of homogeneous equations with respect to the amplitudes в0 and h0 of the oscillations:

[Ah + Mhfc2(l – Kl)]h0 + 0o[Ae + Mhk2(xe – rrcg)] = 0, (12.10)

[Bh + fihk2(xe – xcg)]h0 + в0[Вв + /ih*efc2(l – «h«eh)] = °- (12-n)

Note that the system written above contains a combined parameter рь = that can be called the reduced density. This parameter was initially introduced in the analysis of dynamic stability; see section 11. The parameters «h and Kffh represent ratios of circular frequencies

a>h xi в

— 5 К eh —

UJ U>h

where cj represents that of free oscillations.

The critical condition of flutter is reached for a combination of Kh and к = loC0/U0, or for a given wing, for a combination of the circular frequency cj and the speed of forward motion f70, when the determinant of the ho­mogeneous system of equations becomes equal to zero. The magnitude of U0 corresponding to the critical condition of flutter may be defined as the speed of flutter and will be designated as Uf. Composing the determinant Л of the system and equating it to zero, we obtain the following equation for determining fth and fc, corresponding to flutter:

A{kh, k) = [Ah(fc) + цьк2( 1 – «£)][£*(*) + Vhiek2(l – K-Weh)}

~[Ae(k) + /uhfc2(xe – xcs)][Bh(k) + nhk2(xe – leg)] — 0.

It is worthwhile mentioning that A is complex-valued. Therefore, setting the determinant to zero means equating to zero both its real and imaginary parts, i. e., ША = 0 and ЭЛ = 0. The latter equations enable us to determine two real quantities «ь and k. It can be seen from the structure of the flutter equation, written above, that it can be rearranged into a quadratic equation with respect to /С =

a(k)K? + 2 b(k)K + c(fc) = 0, (12.14)

where the coefficients a(fc), b(k), and c(k) are complex-valued functions of the Strouhal number k, given by the formulas

a(k) = a3a5^h, c(k) = (a2 + a3)(a4 + a5) – ab

b(k) = -^[a3(a4 + a5) + ^ha5(a2 +a3)], where a, i = сц(к),і = 1 • • • 5 are written below:

ai(fc) = [Ah(k) + /іьk2(xe – xcg)][Bh(k) + /іьk2(xe – scg)], a2(k) = Ah(k),

a3(fc) = /ihfc2, a4(fc) = Bg(k), a5(fc) = /іьгеА:2.

Separating the real and imaginary parts in (12.14), we obtain the following two equations with respect to JC =

Ua(k)JC2 + 2 m(k)K + Щк) = 0, 2 Щк)К, + Qc(k) = 0. (12.15)

-m(k) ± ^m[75](k) – Щк) ~ Щк)

Selecting the appropriate root of the quadratic equation and equating it to the solution of the linear equation, we can solve the resulting relationship2 with respect to к = kf and, consequently, find the corresponding magnitude of /С = /Cf = Then the speed of flutter Uf can be determined in the

The first of these equations with real-valued coefficients is still quadratic, whereas the second is linear in JC. The solution with respect to /С is straight­forward

Equation (12.17) enables us to evaluate the speed of flutter for a given circular frequency u>h of the heave spring and the chord length C0 of the foil. For similarity considerations it is convenient to form a nondimensional speed of flutter Uf. This can be done by relating Uf to the quantity uj^Cq which has the dimension of speed. The resulting expression can be written as

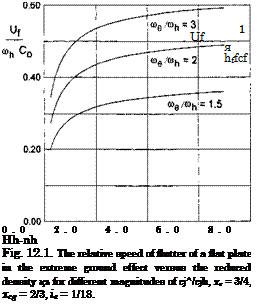Some calculated results for the two-dimensional flutter of a flat plate in the extreme ground effect are presented in Fig. 12.1 in form of a graph, showing the behavior of the nondimensional speed of flutter versus the reduced density /ih = fih for different ratios of the circular frequencies of the pitch and heave springs tt<9h = ujq/uj^. These results correspond to the following magnitudes of input quantities: xe = 3/4, xcg = 2/3, ie = 1/18. One can observe from the graph that for a considered a decrease in the reduced density /іь leads to a diminution of the speed of flutter. It is remarkable that in the extreme ground effect, the influence of the relative ground clearance h and the density of the wing /і, which are combined in just one parameter /іь, are somewhat similar. For example, the same relative reduction of either h or (i entails an identical drop in the speed of flutter. If the same wing flies closer to the ground, its speed of flutter becomes smaller, i. e., the proximity of the ground reinforces flutter-related restrictions upon the speed of the vehicle as compared to flight in unbounded air.