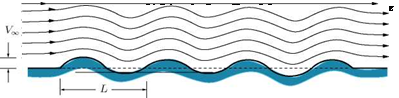
Compressible Subsonic Flow

The governing equation for this flow is:

(1 — МОТ)фХХ + Fz = °.

Solving as before, we get the result:

ф(х, z) = — = exp — kz^J 1 — M2 cos(kx)

1 — M2a

Hence, we have:

9.25.3 Supersonic Flow

For supersonic flow the governing potential equation is:

(M2 — 1) фхх — Фzz = 0.

For this equation, by Equation (9.196), we have the solution as:

ф(х, z) = f (x — Pz) + g(x + Pz),

where в = cot Ц, = M2 — 1.

From the geometry of the problem under consideration, since the disturbances can move only in the direction of flow, there can be only left-running Mach lines, as shown in Figure 9.41(c). Therefore:

ф(х^) = f (x — Pz), g = 0.

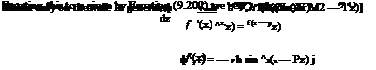Hence, the perturbation velocity w on the wall is

Therefore:

The ф here is only the disturbance potential, and if the total potential is required, add (Vlx) to ф.