An Aeroelastic Wing in the Extreme Ground Effect

Efremov [70]—[72] was one of the first to analyze at length important matters of the static and dynamic aeroelasticity of a lifting surface in proximity to the ground. We consider first a wing of infinite aspect ratio. Then, in the
case of static aeroelasticity, the elastic deflections of the foil contour can be determined by the simplified equation

f, i‘I – dV _ +

da?-tm=v ~P

with boundary conditions (for a freely supported plate)

m-m-gm-gw-*.

where T is the stretching longitudinal force, T = 2T/pU„C0 and p~ — p+ is the nondimensional pressure difference across the foil, causing its deformation f(x).

We consider an infinitely thin foil in the extreme ground effect. Recalling the material of section 3, we can formulate the following (linear) problem for determining the pressure difference (aerodynamic loading) p~ — cor­responding to the flow past an elastic foil with a distribution of ordinates ys(x) = y0(x) + /(x), where y0(x) characterizes the basic configuration of the foil and /(x) gives the perturbed displacements of points on the foil due to elasticity:

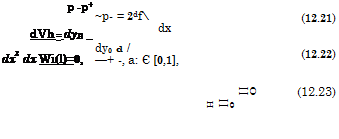where (рг is the perturbed velocity potential in the channel flow.

It is assumed that in the course of elastic deformation, the end points of the foil (leading and trailing edges) remain in the same positions, i. e., 2/s(l) = 2/o(l) and ys(0) = y0(0) or, in other terms, /(0) = /(1) = 0. Representing the perturbation velocity in the channel flow as a sum

dK _ <H dyi,

dx dx dx

with terms corresponding to the basic foil configuration and its perturbation, we can integrate (12.22), accounting for the Kutta-Zhukovsky condition, to obtain

= [Vo(x) – 2/o(0) + f(x),

wherefrom

(12.24)

Now, it is possible to replace the right-hand side of equation (12.19), using expression (12.24). The resulting equation has the form

D— – T— – -/ = 0.

dx4 dx2 hJ

Determination of the condition of the occurence of the static instability of an elastic foil can be reduced to finding eigenvalues of a two-point homogeneous boundary problem, comprising equations (12.25) and (12.20). First, we con­sider particular cases. For D = 0, we deal with a membrane foil, and the corresponding stability equation takes the form

Т~л + / = °> (12.26)

The eigenvalues and eigen forms of the foil that comply with problem (12.26),

(12.20) can be easily found to be

ATn = (^Т/Г) =ШГ’ fn(x) = sin гига:. (12.28)

As seen from this result, the loss of stability of a membrane foil occurs at a certain critical speed, whose minimal magnitude can be associated with the speed of divergence UQd. Relating the speed of divergence to the quantity y/T/pC0, which also has a dimension of speed, and setting n = 1, we can derive the following expression for the nondimensional speed of divergence

UQd:

U0d = ^== = 7rVh. (12.29)

Up* VWpc!

v^Y pCо

Another concrete case can be obtained for a purely elastic foil when T = 0,D ф 0. In this case, the divergence condition can be deduced from the equation •D. 2 f — о dx* d/ “ II II Q Ipu2co3 V hD (12.30) and (12.20) in the form Ad„ = п2тг2, (n = 1,2.. ■), (12.31)

Deriving eigenvalues for the more general equation (12.25), rewritten in the form

7Г*

(12.33) It is easy to see that in particular cases when D = 0,T ф 0 and and T = 0,D ф 0, expression (12.33) yields the previous results of (12.29) and (12.32). Comparison of (12.33) and (12.32) indicates that when an elastic foil is subject to the action of stretching tension (T > 0), the loss of static sta­bility occurs at higher speeds.[76] It is important to emphasize that for h —> 0, the speed of divergence of elastic foil is proportional to the square root of the relative ground clearance. An analysis of the mathematical model of dynamic aeroelasticity with the pronounced effects of lag both in terms of aerodynamic loads and elastic deflection in the extreme ground effect leads to the following generalized equations of free (eigen) oscillations of a flexible foil in the vicinity of solid ground:[77]

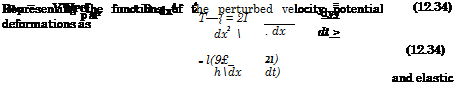and subject to conditions (12.20), we obtain the following formula for the relative speed of an divergence of elastic foil under tension:

4>h (x> t) = Фі (x) exp(ikt), f(x, t) = f(x) exp(ita), (12.36)

where к = ujCq/U0 is the Strouhal number, і = >/“ї and eliminating px from the previous two equations, we obtain the following homogeneous ordinary differential equation of the sixth order with respect to f(x):

(12.37)

Taking f(x) — /о ехр(ірж), p = П7Г, we obtain the following characteristic equation:

Dpe + Tp4 – 2^—5tk2 + хУ + ^ + X = O’ (12‘38)

It is convenient to rearrange equation (12.38) as a quadratic equation with respect to the eigen magnitudes of the Strouhal number к:

ijs‘+1k)k2-jk~ Л0*’+- D=■<12’39»

Solving this equation for к = kn, we obtain

(12.40)

The minimal magnitude of the speed U0, which turns the expression under the square root into zero, can be associated with speed of flutter; see [71]. The resulting expression for the relative (minimal) speed of flutter U0t can be found from (12.40) for n = l, p = p = 7Г in the form

One can see from equation (12.41) that the speed of flutter diminishes as the relative ground clearance tends to zero. The Strouhal number fcf, corresponding to the flutter condition, is given by the expression

To a certain extent, the asymptotics of the extreme ground effect furnish an analog of the “piston theory” and permit us to evaluate the magnitudes of the critical speeds.

In a similar fashion, we can analyze the static stability of a wing of finite aspect ratio in motion close to the ground. For example, following the lines of the approach discussed above, the problem of the membrane wing in flow is reduced to the problem of the stability of a flexible plate subject to the action of tensile forces. In the latter case, the problem of eigen solutions is governed by the equation

– 9 d2f

Taaf+hd‘° (1243)

and corresponding boundary conditions. An analysis of the dynamic stability of an elastic lifting surface can be carried out on the basis of the equation

DAAAf – TAAf – 2—6tk2Af – + + Щ-j – 0, (12.44)

p h h ox h

where / = /(x, z) is a complex function of two independent variables.

Efremov also examined the influence of compressibility upon the charac­teristics of flexible foils. It was shown that at supersonic speeds the flexibility of the foil can give rise to an additional wave drag. In the case of subsonic flexible foil at small distances from the ground, a differential equation was obtained, describing the complex interaction of longitudinal elastic waves of deformation and acoustic waves in the gas.