. Generation of Broadband Sound Waves with a Prescribed Spectrum by an Energy-Conserving Discretization Method

where x (ш) is a random-phase function, a0 is the speed of sound, and А(ш) is the amplitude function.

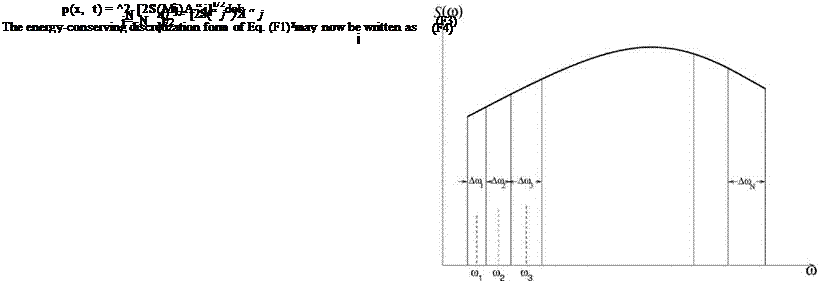
For numerical computation, the spectrum S(ш) has to be discretized. A simple way is to divide the spectrum into narrow bands with bandwidth Дшj for the jth band. The bandwidths need not be constant. Let the center frequency of the jth band be ш j. To avoid harmonic interaction, it will be required that no center frequency is the harmonic of another, i. e., ojj = Кшк, j = k, K = integer.

A spectrum is a distribution of acoustic energy with respect to frequency. The energy in the jth band is S(oij )Дш j as Дш j ^ 0. Now, for small Дш j, a reasonable approximation is to assume that the energy in the jth band is concentrated in the center frequency шj. That is, the jth band is approximated by a single wave in the following form:

A more formal way of stating the approximation is to replace the amplitude function А(ш) of Eq. (F1) by a row of delta functions, i. e.,

TO

А(ш) = ^2, Aj8(ш — шj) (F2)

j=—TO

The energy of a discrete frequency wave is equal to 1 Ajj. Thus, to conserve energy, it is necessary to require

2 Aj = S(ш)Дш j.

where xj is a random number, specifically x-j = xj.

Now, the two-point space-time correlation function of the sound wave field given by Eq. (F4) is

p(x’, t’)p(x", t’ + t)

NN

= 2[S(“j)S(rnk)A<»j A“] ^

(F5)

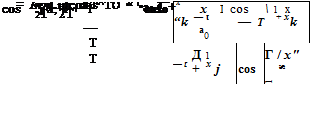where the overbar denotes a time average. Consider, for the moment, the time – averaged terms on the right side of Eq. (F5).

This time average is equal to zero except when k = j. In this special case, by expanding the second cosine term on the right side by compound angle formula, it is readily found that

where 5 jk is the Kronecker delta. Therefore, Eq. (F5) reduces to

The autocorrelation function of the wave field may be found by setting x" = x’ in Eq. (F7). This yields

N

p(x’, t’)p(x’, t’ + t) = ^2 S(«k)A«k cos(«kT).

k=—N

The power of the acoustic field is given by setting T = 0. Thus,

_______ N ^

p2 (x’, t) = E S(rnk)A«k ^ / S(«)d«; in the limit A«k ^ 0. (F9)

U Л Г *

Eq. (F9) indicates that S(«) is the spectrum of the wave field.

Another way to find the spectrum is to make use of the fact that the spectrum is the Fourier transform of the autocorrelation function. That is, if S(«) is the spectrum of the wave field given by Eq. (F4), then it is equal to the Fourier transform of the right side of Eq. (F8) as follows:

L N

— 1C N

S(«) = — I ^2 S(«k)A«kcos(«kT)e’«TdT.

Ж-L k=-N

In the limit A«k ^ 0,

L L

S(«) = 2П // S(Q) cos(^T)e’«T dT dQ,

1

= 2[S(«) + S(-«)] = S(«).

The usual symmetry assumption, i. e., S(-«) = S(«) is assumed here.

A special case of interest is the sound field associated with a broadband monopole source. Let (У, в,ф) be the spherical coordinates system centered at the monopole. Y is the radial coordinate (see Figure 14.12). The sound field according to the energy conserving discretization procedure is