DATA ACQUISITION AND SAMPLING OF SIGNALS

This is an important ingredient of the total flight testing, simulation, and estimation exercises. For successful data analysis a good set of data should be generated, gathered, and recorded or telemetered. The data acquisition personnel and data analysts should keep several aspects in mind: (1) How the data got to the analysis program from the sensors and how the data were filtered, (2) How the data were digitized, time tagged, and recorded, and (3) For extracting more information from data as much information as available from the related sources should be recor – ded/gathered. This requires a systems approach. This is to say that one should look at the entire system from input to output because the connections and interactions between various components are of varied nature and importance. One should safeguard against over reliance on misleading simulation, unforeseen circumstances, and neglect of the synergism of data system problems.

In most of the flight mechanics modeling and analysis exercises, digitized data are required. It is important to see that the sampling rate is properly selected so that there is no loss of useful information and that the burden of collecting too much data does not increase. It is based on the Nyquist theory, which applies to many different fields where data are captured. In general terms, it states the minimum number of resolution elements required to properly describe or sample a signal. In order to reconstruct (interpolate) a signal from a sequence of samples, sufficient samples must be recorded to capture the peaks and trough of the original waveform. For example, when a digital recording uses a sampling rate of 50 kHz, the Nyquist frequency is 25 kHz. If a signal that is sampled contains frequency components that are above the Nyquist limit, aliasing will be introduced in the digital representation of the signal unless those frequencies are filtered out before digital encoding. The Nyquist sampling theorem states that a sample with a regular sample interval of T seconds (a sample rate of 1/T samples/s) can contain no information at a frequency higher than 1/(2T) Hz. This limit frequency is called the Nyquist frequency, the half-sample frequency, or the folding frequency. Frequency limits of 12.5 or 25 Hz (25 or 50 samples/s) are sufficient to include all useful aircraft stability and control informa­tion on the modes/data. The higher frequencies in the original continuous-time signal could contain (1) structural resonance modes, higher than the rigid body dynamic modes, (2) AC (altering current) power frequencies, (3) engine vibration modal responses, and (4) thermal noise and other nuisance data. These high-frequency data shift to an apparent lower frequency and this phenomenon is called aliasing or frequency folding (Nyquist folding). The high-frequency noise/data contaminate the low-frequency stability and control data. After sampling there is no way to remove

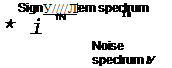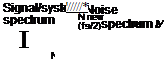Low frequency—affected FIGURE C2 Frequency aliasing.

the effect of this aliasing, and hence the data should be adequately treated before sampling. The effective method is to apply pre-sample filtering to the data. This means filtering the signal (+noise, or unwanted higher frequency data) to remove the high-frequency/unwanted data/responses before the actual sampling is performed. To avoid the aliasing effect, (1) pre-filter the data before digitization, so that unwanted signals in the higher band that would otherwise aliase the low frequencies would be eliminated; however, the pre-filtering would introduce lags in signal, so the time lag should be accounted for and (2) sample the signal at a very high rate, so that the folding frequency is moved farther away and the high-frequency signals (noise, etc.) would alias the frequencies that are near the new folding frequency, which is farther away from the system/signal frequency of interest. This assures that the useful low-frequency band signals are not affected, as can be seen from Figure C2.

However, it is prudent to sample the aircraft responses at 100 or 200 samples/s and then digitally filter the data and thin it to 25 or 50 samples/s. The pre-sample filter requirements are (1) a low-pass filter at 40% of the Nyquist frequency can be used, (2) for systems with high sampling rates, a first-order filter would be adequate, and (3) for low sample rate systems higher-order filters may be necessary.

In the digitized signal, the resolution is exactly one count, and if the resolution magnitude is much smaller than the noise level of the digitized signal, the resolution problem is a non-issue. A good resolution is 1/100 of the maneuver size and a low resolution is acceptable for Euler angles, say, 1/10 of the maneuver size. The time tagging of data is very important. The time errors, in data measurements, would affect the accuracy of estimated derivatives depending on the severity of these errors. ‘‘Time tagging’’ refers to the information about the time of each measurement. Any time lag due to analog pre-filtering or sensors should be taken into account; otherwise, it would cause errors in time tag. Some derivate estimates are extremely sensitive to time shifts in certain signals. Time errors >0.01 s may cause problems, whereas accuracy of 0.02-0.05 s is usually tolerable for signals like altitude and airspeed.