Phugoid Motion

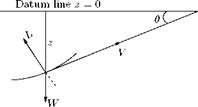
A phugoid is the path of a particle which moves under gravity in a vertical plane and which is acted upon by a force L normal to the path and proportional to V2.

Since no work is done by force L, it follows that (1V2 — gz), the total energy of the particle (per unit mass), is constant, z being the depth of the particle below horizontal line, when speed is V, as shown in Figure 10.11.

We can choose the position of this line so that the constant energy is zero, and then we shall have:

V2 = 2gz. (10.6)

If в is the inclination of the path to the horizontal, as in Figure 10.11, then:

W V2

L — W cos в =———- ,

g R’

where R is the radius of curvature.

If we could imagine an aircraft flying at constant incidence, and so arrange that the thrust exactly balances the drag, the center of gravity of the aircraft would describe a phugoid, for such a case L = 2pV2SCL and CL is constant for an incidence (if we neglect the effect of curvature of the path on lift coefficient).

Now let us assume that V1 is the speed at which the aircraft would fly in steady straight horizontal flight at the same incidence as in the phugoid. Then:

12

W = 2 pV2SCl

so that Equation (10.7) will give:

V2 V2 —„ — cos в = — V2 gR

by Equation (10.6), V2 = 2gz, V2 = 2gz1, therefore the above equation becomes: z a 2z —– cos в = —– . z1 R Now if ds is an element of the arc of the path in Figure 10.11, then: 1 de dz — = —, sin в =———- . R ds ds Therefore Equation (10.8) can be written in the equivalent form as follows:

(10.8)

(10.9)

d (z 2 cos") = H 1 1 z 2 z 2 cos в =——————- s—+ constant 2z1 § 1 z constant cos в = —————— 1—— 1—- . 3 z1 z 2 Now let us assume that the “constant” to be C„Jz. Therefore:

1 z z1 cos в =——— + C W —. 3 z1 V z

(10.10)

Let us differentiate this with respect to в:

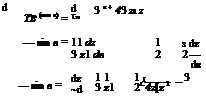From Equation (10.9), we have sin в

dz dz 1 C _s/zr dS = Тв 3І7 — "2 ~

or

dB 1 C _s/zr

ds 3z1 2 z 2

Datum Figure 10.12 Phugoid along a horizontal straight line.

Datum

Figure 10.13 An aircraft in trochoidal-like paths.

1 _ _1____ C yZT

R = 3z1 2 ^ 2

or

Z1 _ 1 C fz R = 3 – 2 Z3′

It can be shown that in Equation (10.10), cos в > 1 if C > 2/3, so that no phugoid is possible.

If C = 2/3, Equation (10.10) gives cos в = 1 so that в = 0 and R = <X). For this condition the phugoid is along a horizontal straight line, at depth z, below the datum line.

If C = 0, Equation (10.11) gives R = 3zi, and the phugoid reduces to a set of semicircles of radius 3zi. The cusps are on the datum line and the paths correspond to unsuccessful attempts at “loop the loop,” as shown in Figure 10.12.

For 0 < C < 2/3, the flight path will become trochoidal-like paths, as shown in Figure 10.13.

If Z1 and the initial values of z and в are prescribed, Equation (10.11) shows that for a given value of C there are two possible radii of curvature owing to the ambiguity sign of the square root. If there is a sudden gust, an aircraft describing a trochoidal-like paths as in Figure 10.13 will get into a loop, as shown in Figure 10.14.