The extension of the computational method, described in Section 3.5, to twodimensional lifting flows is described in this section. The basic panel method was developed by Hess and Smith at Douglas Aircraft Co. in the late 1950s and early 1960s. The method appears to have been first extended to lifting flows by Rubbert[19] at Boeing. The two-dimensional version of the method can be applied to aerofoil sections of any thickness or camber. In essence, in order to generate the circulation necessary for the production of lift, vorticity in some form must be introduced into the modelling of the flow.
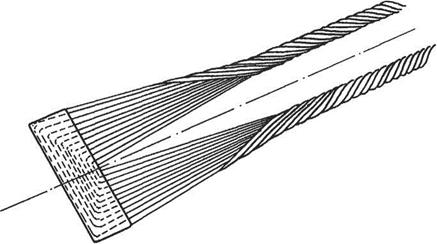
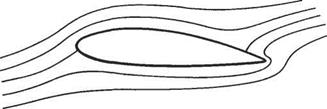
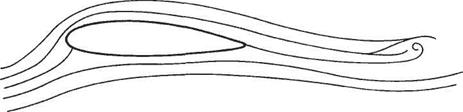
It is assumed in the present section that the reader is familiar with the panel method for non-lifting bodies as described in Section 3.5. In a similar way to the computational method in the non-lifting case, the aerofoil section must be modelled by panels in the form of straight-line segments – see Section 3.5 (Fig. 3.37). The required vorticity can either be distributed over internal panels, as suggested by Fig. 4.22a, or on the panels that model the aerofoil contour itself, as shown in Fig. 4.22b.
The central problem of extending the panel method to lifting flows is how to satisfy the Kutta condition (see Section 4.1.1). It is not possible with a computational scheme to satisfy the Kutta condition directly, instead the aim is to satisfy some of the implied conditions namely:
(a) The streamline leaves the trailing edge with a direction along the bisector of the trailing-edge angle.
(b)
As the trailing edge is approached the magnitudes of the velocities on the upper and lower surfaces approach the same limiting value.
|
|
|
|
|
|
|
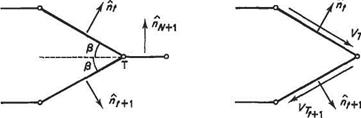
Fig. 4.23 Two methods of implementing the Kutta condition at the trailing edge T
|
|
(c) In the practical case of an aerofoil with a finite trailing-edge angle the trailing edge must be a stagnation point so the common limiting value of (b) must be zero.
(d) The source strength per unit length must be zero at the trailing edge.
Computational schemes either use conditions (a) or (b). It is not generally possible to satisfy (c) and (d) as well because, as will be shown below, this leads to an overspecification of the problem. The methods of satisfying (a) and (b) are illustrated in Fig. 4.23. For condition (a) an additional panel must be introduced oriented along the bisector of the trailing-edge angle. The value of the circulation is then fixed by requiring the normal velocity to be zero at the collocation point of the additional (N + l)th panel. For condition (b) the magnitudes of the tangential velocity vectors at the collocation points of the two panels, that define the trailing edge, are required to be equal. Hess[20] has shown that the use of condition (b) gives more accurate results than (a), other things being equal. The use of surface, rather than interior, vorticity panels is also preferable from the viewpoint of computational accuracy.
There are two main ways that surface vorticity panels can be used. One method* is to use vorticity panels alone. In this case each of the N panels carries a vorticity distribution of uniform strength per unit length, 7i(i —1,2, …, N). In general, the vortex strength will vary from panel to panel. Let і = t for the panel on the upper surface at the trailing edge so that 1 = t + 1 for the panel on the lower surface at the trailing edge. Condition (b) above is equivalent to requiring that
 It = -7/+1
It = -7/+1
The normal velocity component at the collocation point of each panel must be zero, as it is for the non-lifting case. This gives N conditions to be satisfied for each of the N panels. So when account is also taken of condition Eqn (4.104) there are N + 1 conditions to be satisfied in total. Unfortunately, there are only N unknown vortex strengths. Accordingly, it is not possible to satisfy all N + 1 conditions. In order to proceed further, therefore, it is necessary to ignore the requirement that the normal velocity should be zero for one of the panels. This is rather unsatisfactory since it is not at all clear which panel would be the best choice.
An alternative and more satisfactory method is to distribute both sources and vortices of uniform strength per unit length over each panel. In this case, though, the vortex strength is the same for all panels, i. e.
 7/ = 7(i= 1,2, N)
7/ = 7(i= 1,2, N)
Thus there are now N + 1 unknown quantities, namely the N source strengths and the uniform vortex strength per unit length, 7, to match the N + 1 conditions. With this approach it is perfectly feasible to use internal vortex panels instead of surface ones. However these internal panels must carry vortices that are either of uniform strength or of predetermined variable strength, providing the variation is characterized by a single unknown parameter. Generally, however, the use of surface vortex panels leads to better results. Also Condition (a) can be used in place of (b). Again, however, the use of Condition (b) generally gives more accurate results.
A practical panel method for lifting flows around aerofoils is described in some detail below. This method uses Condition (b) and is based on a combination of surface vortex panels of uniform strength and source panels. First, however, it is necessary to show how the normal and tangential influence coefficients may be evaluated for vortex panels. It turns out that the procedure is very similar to that for source panels.
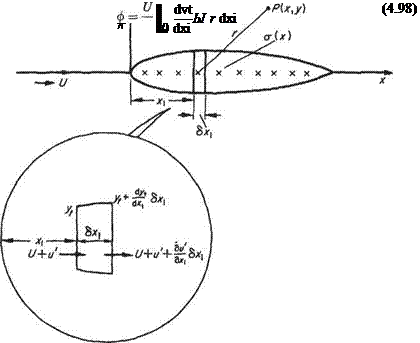
The velocity at point P due to vortices on an element of length <5£ in Fig. 4.24 is given by
 sve = ldt
sve = ldt
where 7d£ replaces Г/(27г) used in Section 3.3.2. SVg is oriented at angle в as shown.
Therefore, the velocity components in the panel-based coordinate directions, i. e. in the xq and y<2 directions, are given by
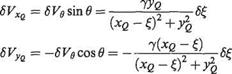 (4.107)
(4.107)
(4.108)
 Д»/2
Д»/2
Fig. 4.24
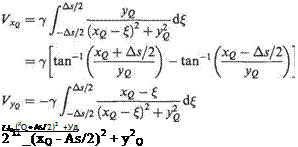 To obtain the corresponding velocity components at P due to all the vortices on the panel, integration along the length of the panel is carried out to give
To obtain the corresponding velocity components at P due to all the vortices on the panel, integration along the length of the panel is carried out to give
(4.109)
(4.110)
Following the basic method described in Section 3.5 normal and tangential influence coefficients, N’y and Ту are introduced, the primes are used to distinguish these coefficients from those introduced in Section 3.5 for the source panels. N’y and Ту represent the normal and tangential velocity components at collocation point і due to vortices of unit strength per unit length distributed on panel j. Let?,■ and л,(і = 1,2, ..N) denote the unit tangent and normal vectors for each of the panels, and let the point P correspond to collocation point i, then in vector form the velocity at collocation point і is given by
VpQ — VXQij + Vya tij
To obtain the components of this velocity vector perpendicular and tangential to panel і take the scalar product of the velocity vector with л,- and?,■ respectively. If furthermore 7 is set equal to 1 in Eqns (4.109) and (4.110) the following expressions are obtained for the influence coefficients
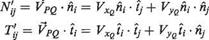 (4.111a)
(4.111a)
(4.111b)
Making a comparison between Eqns (4.109) and (4.111) for the vortices and the corresponding expressions (3.97) and (3.99) for the source panels shows that
With the results given above it is now possible to describe how the basic panel method of Section 3.5 may be extended to lifting aerofoils. Each of the N panels now carries a source distribution of strength at per unit length and a vortex distribution of strength 7 per unit length. Thus there are now N + 1 unknown quantities. The N x N influence coefficient matrices Ny and Ту corresponding to the sources must now be expanded to N x (N + 1) matrices. The (N + l)th column now contains the velocities induced at the collocation points by vortices of unit strength per unit length on all the panels. Thus Nys+i represents the normal velocity at the zth collocation point induced by the vortices over all the panels and similarly for 7) л’-і – Thus using Eqns (4.111)

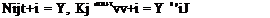
 (4.113)
(4.113)
In a similar fashion as for the non-lifting case described in Section 3.5 the total normal velocity at each collocation point, due to the net effect of all the sources, the vortices and the oncoming flow, is required to be zero. This requirement can be written in the form:
 (4.114)
(4.114)
These TV equations are supplemented by imposing Condition (b). The simplest way to do this is to equate the magnitudes of the tangential velocities at the collocation point of the two panels defining the trailing edge (see Fig. 4.23b). Remembering that the unit tangent vectors І, and tt+ are in opposite directions Condition (b) can be expressed mathematically as
N ^ ^
Y vjTtj + 7Г, д+і + U ■ І, = — Y + 7Г;+ід+1 + U • t,+1J (4.115)
Equations (4.114) and (4.115) combine to form a matrix equation that can be written as
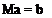 (4.116)
(4.116)
where M is an (TV + 1) x (TV + 1) matrix and a and b are (TV + 1) column vectors. The elements of the matrix and vectors are as follows:
MU = NU і = 1,2, …,N j — 1,2,… ,7V + 1
Mn+j = TtJ + Tt+j j = 1,2,…, TV +1
a,- = <7,- ;= 1,2,…,7V and ajv+i = 7
bt = —U ■ ht /=1,2,…,7V
Ья-и = —U ■ (it + ?;+i)
Systems of Unear equations Uke (4.116) can be readily solved numerically for the unknowns at using standard methods (see Section 3.5). Also it is now possible to see why the Condition (c), requiring that the tangential velocities on the upper and lower surfaces both tend to zero at the trailing edge, cannot be satisfied in this sort of numerical scheme. Condition (c) could be imposed approximately by requiring, say, that the tangential velocities on panels t and t + 1 are both zero. Referring to Eqn (4.115) this approximate condition can be expressed mathematically as
‘Y. OjT. j + 77^1 + U ■ І, — 0
Y’. <rjT,+yj + 77)+i^+i + U ■ tt+i — 0 7=1
Equation (4.115) is now replaced by the above two equations so that M in Eqn
(4.116) is now a (N + 2) x (N + 1) matrix. The problem is now overdetermined, i. e. there is one more equation than the number of unknowns, and Eqn (4.116) can no longer be solved for the vector a, i. e. for the source and vortex strengths.
The calculation of the influence coefficients is at the heart of a panel method. In Section 3.5 a computational routine in FORTRAN 77 is given for computing the influence coefficients for the non-lifting case. It is shown below how this routine can be extended to include the calculation of the influence coefficients due to the vortices required for a lifting flow.
Two modifications to SUBROUTINE INFLU in Section 3.5 are required to extend it to the lifting case.
(1) The first two execution statements i. e.
DO 10 I = 1,N
10 READ(7,*) XP(I),YP(I)
should be replaced by
NPl =N+1 DO 10 I = 1,N AN(I, NPl) = 0.0 AT (I, NPl) = PI 10 READ(7,*)XP(I),YP(I)
The additional lines initialize the values of the influence coefficients, Nittf+1 and і in preparation for their calculation later in the program. Note that the initial value of TitN+1 is set at 7г because in Eqn (4.113)
^N+l, N—1 — % :
that is the tangential velocity induced on a panel by vortices of unit strength per unit length distributed over the same panel is, from Eqn (4.112), the same as the normal velocity induced by sources of unit strength per unit length distributed over the panel. This was shown to take the value tv in Eqn (3.100b).
(2) It remains to insert the two lines of instruction that calculate the additional influence coefficients according to Eqn (4.113). This is accomplished by inserting two additional lines below the last two execution statements in the routine, as shown
AN(I, J) = VX * NTIJ + VY * NNIJ Existing line
AT (I, J) = VX * TTIJ + VY * TNI J Existing line
AN (I, NPl) = AN (1, NPl) + VY * NTI J – VX * NNIJ New line ДТ(І, NPl) =AT(I, NPl) + VY * TTI J – VX * TNI J Newline
As with the original routine presented in Section 3.5 this modified routine is primarily intended for educational purposes. Nevertheless, as is shown by the example computation for a NACA 4412 aerofoil presented below, a computer program based on this routine and LU decomposition gives accurate results for the pressure distribution and coefficients of lift and pitching moment. The computation times required are typically a few seconds using a modern personal computer.
The NACA 4412 wing section has been chosen to illustrate the use of the panel method. The corresponding aerofoil profile is shown inset in Fig. 4.25. As can be seen it is a moderately thick aerofoil with moderate camber. The variation of the pressure coefficient around a NACA 4412 wing section at an angle of attack of 8 degrees is presented in Fig. 4.25. Experimental data are compared with the computed
|
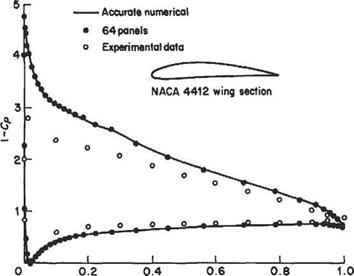
Fig. 4.25 Variation of pressure coefficient around a NACA 4412 wing section at an angle of attack of 8°
|
results for 64 panels and 160 panels. The latter can be regarded as exact and are plotted as the solid line in the figure. It can be seen that the agreement between the two sets of computed data is very satisfactory. The agreement between the experimental and computed data is not good, especially for the upper surface. This is undoubtedly a result of fairly strong viscous effects at this relatively high angle of attack. The discrepancy between the computed and experimental pressure coefficients is particularly marked on the upper surface near the leading edge. In this region, according to the computed results based on inviscid theory, there is a very strong favourable pressure gradient followed by a strong adverse one. This scenario is very likely to give rise to local boundary-layer separation (see Section 7.4.1 below) near the leading edge leading to greatly reduced peak suction pressures near the leading edge.
The computed and experimental lift and pitching-moment coefficients, CL and СМці are plotted as functions of the angle of attack in Fig. 4.26. Again there is good agreement between the two sets of computed results. For the reasons explained above the agreement between the computed and experimental lift coefficients is not all that satisfactory, especially at the higher angles of attack. Also shown in Fig. 4.25 are the predictions of thin-aerofoil theory – see Eqns (4.91) and (4.92). In view of the relatively poor agreement between theory and experiment evidenced in Fig. 4.26 it might be thought that there is little to choose between thin-aerofoil theory and computations using the panel method. For predictions of Cl and Cmva this is probably a reasonable conclusion, although for aerofoils that are thicker or more cambered than the NACA 4412, the thin-aerofoil theory would perform much less well. The great advantage of the panel method, however, is that it provides accurate results for the pressure distribution according to inviscid theory. Accordingly, a panel method can be used in conjunction with a method for computing the viscous (boundary-layer) effects and ultimately produce a corrected pressure distribution that is much closer to the experimental one (see Section 7.11).
|
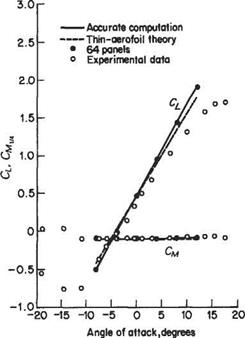
Fig. 4.26 Variation of lift and moment coefficients with angle of attack for NACA 4412 aerofoil
|
Exercises
1 A thin two-dimensional aerofoil of chord c is operating at its ideal lift coefficient Си – Assume that the loading (i. e. the pressure difference across the aerofoil) varies linearly with its maximum value at the leading edge. Show that
where yc defines the camber line, a is the angle of incidence, and £ = xjc.
[Hint: Do not attempt to make the transformation x = (c/2)(l — cos 0), instead write the singular integral as follows:
Ґ—!—d£ = lim{ Ґ ‘-l-d£+ Ґ —Ц-d*}]
Jo г-оіУо £-£i Jti+e£-£i J
Then, using this result, show that the angle of incidence and the camber-line shape are given by
»=£; &=^{-(i-£)!in(,-0+£«-2)i„f}
[Hint: Write —1 = C—1 — C where 1 + C = 2ivalCL and the constant C is determined by requiring that yc = 0 at £ = 0 and £ = 1.]
2 A thin aerofoil has a camber line defined by the relation yc = kc£(£ — l)(f – 2). Show that if the maximum camber is 2% of chord then к — 0.052. Determine the coefficients of lift and pitching moment, i. e. Cl and СщА, at 3° incidence.
(Answer: 0.535, —0.046)
3 Use thin-aerofoil theory to estimate the coefficient of lift at zero incidence and the pitching-moment coefficient Сд/1/4 for a NACA 8210 wing section.
(Answer: 0.789, —0.172)
4 Use thin-aerofoil theory to select a NACA four-digit wing section with a coefficient of lift at zero incidence approximately equal to unity. The maximum camber must be located at 40% chord and the thickness ratio is to be 0.10. Estimate the required maximum camber as a percentage of chord to the nearest whole number. [Hint: Use a spreadsheet program to solve by trial and error.]
(Answer: NACA 9410)
5 Use thin-aerofoil theory to select a NACA four-digit wing section with a coefficient of lift at zero incidence approximately equal to unity and pitching-moment coefficient CMvA = -0.25. The thickness ratio is to be 0.10. Estimate the required maximum camber as a percentage of chord to the nearest whole number and its position to the nearest tenth of a chord. The CL value must be within 1% of the required value and СМщ within 3%. [Hint: Use a spreadsheet program to solve by trial and error.]
(Answer: NACA 7610, but NACA 9410 and NACA 8510 are also close.)
6 A thin two-dimensional flat-plate aerofoil is fitted with a trailing-edge flap of chord lOOe per cent of the aerofoil chord. Show that the flap effectiveness,
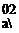 ас,
ас,
Эц
ас,
da where a is the angle of incidence and 77 is the flap angle, is approximately 4у/ё/тг for flaps of small chord.
7 A thin aerofoil has a circular-arc camber line with a maximum camber of 0.025 chord. Determine the theoretical pitching-moment coefficient Сдг1/4 and indicate methods by which this could be reduced without changing maximum camber.
The camber line may be approximated by the expression
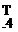
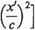 yc = kc
yc = kc
where xl = x — 0.5c. (Answer: —0.0257t)
8
The camber line of a circular-arc aerofoil is given by
Derive an expression for the load distribution (pressure difference across the aerofoil) at incidence a. Show that the zero-lift angle ao = —2h, and sketch the load distribution at this incidence. Compare the lift curve of this aerofoil with that of a flat plate.
9 A flat-plate aerofoil is aligned along the x-axis with the origin at the leading edge and trailing edge at x = c. The plate is at an angle of incidence a to a free stream of
air speed U. A vortex of strength Гу is located at (xv, yv). Show that the distribution, k(x), of vorticity along the aerofoil from x = 0 to x = c satisfies the integral equation
-L [‘«£Ldx = – Ua–hi*’ –
2ir J0 x – x (jcv – xi)2 + уі
where x = x is a particular location on the chord of the aerofoil. If xy = c/2 and у у = А» xv show that the additional increment of lift produced by the vortex (which could represent a nearby aerofoil) is given approximately by
4Г
37ГЙ2 ‘














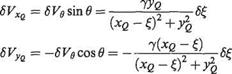 (4.107)
(4.107)
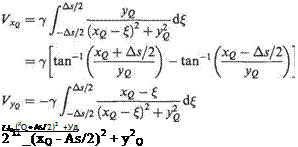 To obtain the corresponding velocity components at P due to all the vortices on the panel, integration along the length of the panel is carried out to give
To obtain the corresponding velocity components at P due to all the vortices on the panel, integration along the length of the panel is carried out to give (4.113)
(4.113) (4.114)
(4.114)


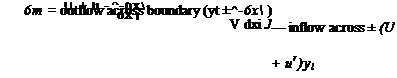

 (4.76)
(4.76)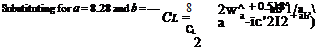
![The normal force and pitching moment derivatives due to pitching[17] The normal force and pitching moment derivatives due to pitching[17]](/img/3130/image603_0.jpg)
![The normal force and pitching moment derivatives due to pitching[17] The normal force and pitching moment derivatives due to pitching[17]](/img/3130/image607.jpg)
![The normal force and pitching moment derivatives due to pitching[17] The normal force and pitching moment derivatives due to pitching[17]](/img/3130/image608.jpg) (4.75)
(4.75)