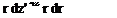In order to see how the calculation of the influence coefficients works in practice, a computational routine written in standard FORTRAN 77 is given below, with a description of each step.
SUBROUTINE INFLU (XC, YC, AN, AT, NHAT, THAT, N, NM)
On exit XC and YC are column matrices of length N containing the co-ordinates of the col locat ion point s; AN and AT are the N*N inf luence coef f icient mat rices; and NHAT and THAT are the N*2 matrices containing the co-ordinates of the unit normal and tangent vectors, the f irst and second columns contain the x and у co-ordinates respectively. N is the number of panels and NM і s the maximum number of panels.
PARAMETER(NMAX=200,PI=3.141592654)
REAL NHAT, NTIJ, NNIJ
DIMENSION XC (NM), YC (NM), AN (NM, NM), AT (NM, NM)
DIMENSION XP (NMAX),YP (NMAX), NHAT (NM, 2 ),
& THAT(NM,2), S(NMAX)
OPEN ( 7 , FILE = ‘ POINTS. DAT ‘ , STATUS = ‘ OLD ‘)
DO 10 I = 1, N Reading in co-ordinates of panel
10 READ(7,*) XP(I), YP(I) end-points.
CLOSE(7)
DO 2 0 J = 1, N IF (J . EQ. 1) THEN XPL = XP(N)
YPL = YP(N)
ELSE
|
XPL = XP (J – 1)
YPL = YP (J — 1)
ENDIF
XC(J) =0.5* (XP(J)+XPL)
YC (J ) =0.5* ( YP { J ) + YPL)
S (J) =SQRT ( (XP ( J) – XPL) **2 + THAT (J, 1) = (XP (J) – XPL) /S (J) THAT(J,2) = (YP(J) – YPL)/S(J) NHAT(J,1) = – THAT(J,2)
NHAT(J,2) = THAT(J,1) CONTINUE
|
Calculating co-ordinates of collocation points.
(YP (J ) —YPL)**2) Calculating panel length. Calculating x co-ordinate of uni t tangent vector. Calculating у co-ordinate of unit tangent vector. Calculating x co-ordinate of unit normal vector. Calculating у co-ordinate of unit normal vector.
Calculation of the influence coefficients.
DO 3 0 I = 1, N DO 4 0 J = 1, N
IF (I. EQ. J) THEN
AN (I, J) = PI Case of і = j.
AT (I, J ) =0.0
ELSE
DX = XC (I) — XC (J) Calculat ing x and у components of line DY = YC(I) — YC(J) joining collocation point iandj
XQ = DX*THAT (J, 1) + DY*THAT (U, 2) Converting to co-ordinate system YQ = DX*NHAT (J, 1) +DY*NHAT(J,2) based on panel j.
VX = 0.5* (LOG ( (XQ + 0.5*S(J) )**2+YQ*YQ ) Using Eqn. (3.97) b —LOG ( (XQ— 0.5*S(J) ) **2 +YQ*YQ) )
VY = ATAN( (XQ+0,5*S (J) )/YQ) – Using Eqn. (3.98)
& A’TAN( (XQ-0.5*S (J) )/YQ)
Begin calculation of various scalar products of unit vectors used in Eqn. (3.99)
NTIJ = C. 0 NNI J = 0.0 TTIJ = 0.0 TNI J= 0.0 DO 50 K = l,2
NT’IJ = NHAT (I, K)*THAT (J, K) + NTIJ NNIJ = NHAT (I, К) *NHAT (J, К) + NNIJ TTI J = THAT (I, K) *THAT (J, K) + TTI J TNI J = THAT (I, K) *NHAT (J, K) + TNI J 5C CONTINUE
End calculation of scalar products.
AN(I, J) =VX*NTIJ + VY*NNIJ Using Eqn. (3.99a)
AN(I, J) =VX*TTIJ + VY*TNIJ Using Sqn. (3.99b)
ENDIF
40 CONTINUE 3 0 CONTINUE RETURN END
The routine, step by step, performs the following.
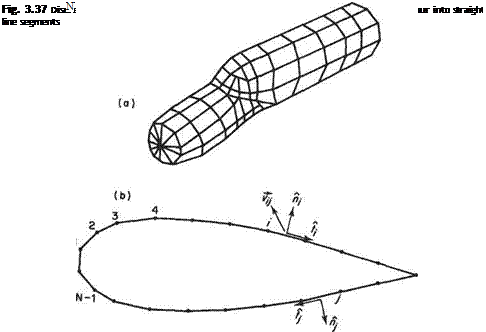
1 Discretizes the surface by assigning numbers from 1 to N to points on the surface of the aerofoil as suggested in Fig. 3.37. The x and у coordinates of these points are entered into a file named POINTS. DAT. The subroutine starts with reading these coordinates XP(f), YP(I), say x!{, y, from this file for 7 = 1 to N.
For each panel from J = 1 to N:
2 The collocation points are calculated by taking an average of the coordinates at either end of the panel in question.
3 The length S(J), i. e. Asj, of each panel is calculated.
4 The x and у components of the unit tangent vectors for each panel are calculated as follows:
J* Asj ’ jr A sj
5 The unit normal vectors are then calculated from % = —tjy and njy = tjx. The main task of the routine, that of calculating the influence coefficients, now begins.
For each possible combination of panels, i. e. 7 and J =[ to N.
6 First the special case is dealt with when і = j, i. e. the velocity induced by the sources on the panel itself at its collocation point. From Eqn (3.93, 3.97, 3.98) it is seen that
vPQx = ln(l) = 0 when xq = yQ = 0 (3.100a)
vpQy tan-1(oo) – tan-1(-oo) = 7Г when xq = yQ = 0 (3.100b)
When і Ф j the influence coefficients have to be calculated from Eqns (3.97,3.98,3.99).
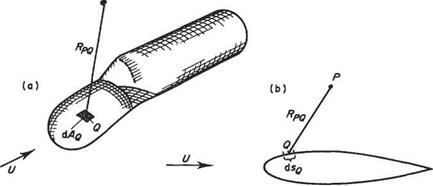
7 The components DX and DY of RPq are calculated in terms of the x and у coordinates.
8 The components of Rpq in terms of the coordinate system based on panel j are then calculated as
Xq = Rpq ■ tj and Yq = Rpq ■ hj
9 VX and VY (i. e. vXg and vyQ) are evaluated using Eqns (3.97) and (3.98).
10 йі ■ tj, Пі ■ hj, ti ■ tj, and /,■ • hj are evaluated.
11 Finally the influence coefficients are evaluated from Eqn (3.99).
The routine presented above is primarily intended for educational purposes and has not been optimized to economize on computing time. Nevertheless, using a computer program based on the above routine and LU decomposition, accurate computations of the pressure distribution around two-dimensional aerofoils can be obtained in a few seconds with a modem personal computer. An example of such a calculation for an NACA 0024 aerofoil is presented in Fig. 3.39. In this case 29 panels were used for the complete aerofoil consisting of upper and lower surfaces.
The extension of the panel method to the case of lifting bodies, i. e. wings, is described in Sections 4.10 and 5.8. When the methods described there are used it is possible to compute the flow around the entire aircraft. Such computations are carried out routinely during aerodynamic design and have replaced wind-tunnel testing to a considerable extent. However, calculation of the potential flow around complex threedimensional bodies is very demanding in terms of computational time and memory. In most cases around 70 to 80 per cent of the computing time is consumed in calculating the influence coefficients. Accordingly considerable effort has been devoted to developing routines for carrying out these calculations efficiently.
|
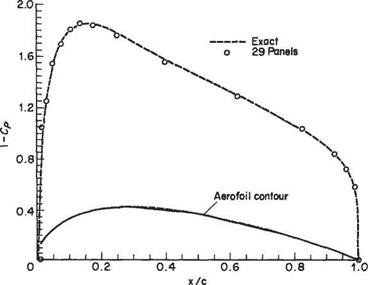
Fig. 3.39 Calculation of pressure coefficient for NACA 0024 aerofoil
|
What are the advantages of the panel method compared to other numerical methods such as finite differences and finite elements? Both of the latter are field methods that require that the whole of the flow field be discretized. The panel method, on the other hand, only requires the discretization of the body surface – the boundary of the flow field. The dimensions of the solution are thereby reduced by one compared to the field method. Thus for the aerofoil calculation presented above the panel method required N node points along the aerofoil contour, whereas a field method would require N x N points throughout the flow field. However, this advantage is more apparent than real, since for the panel method the N x N influence coefficients need to be calculated. The real advantages of panel methods he elsewhere. First, Uke finite-element methods, but unlike finite difference methods, the panel method can readily accommodate complex geometries. In fact, an alternative and perhaps more appropriate term to panel method is boundary-element method. This name makes the connection with finite elements more clear. A second advantage compared to any field method is the ease with which panel methods can deal with an infinite flow field; note that the aerofoil in Fig. 3.39 is placed in an airflow of infinite extent, as is usual. Thirdly, as can readily be seen from the example in Fig. 3.39, accurate results can be obtained by means of a relatively coarse discretization, i. e. using a small number of panels. Lastly, and arguably the most important advantage from the viewpoint of aerodynamic design, is the ease with which modifications of the design can be incorporated with a panel method. For example, suppose the effects of under-wing stores, such as additional fuel tanks or missiles, were being investigated. If an additional store were to be added it would not be necessary to repeat the entire calculation with a panel method. It would be necessary only to calculate the additional influence coefficients involving the new under-wing store. This facihty of panel methods allows the effects of modifications to be investigated rapidly during aerodynamic design.
Exercises
1 Define vorticity in a fluid and obtain an expression for vorticity at a point with polar coordinates (г, в), the motion being assumed two-dimensional. From the definition of a Une vortex as irrotational flow in concentric circles determine the variation of velocity with radius, hence obtain the stream function (ip), and the velocity potential (ф), for a line vortex. (U of L)
2 A sink of strength 120 m2s 1 is situated 2 m downstream from a source of equal
strength in an irrotational uniform stream of 30 m s’1. Find the fineness ratio of the oval formed by the streamline ip = 0. (Answer: 1.51)(CU)
3 A sink of strength 20 m2 s-1 is situated 3 m upstream of a source of 40 m2 s 1, in a uniform irrotational stream. It is found that at the point 2.5 m equidistant from both source and sink, the local velocity is normal to the line joining the source and sink. Find the velocity at this point and the velocity of the undisturbed stream.
(Answer: 1.02ms-1, 2.29ms_1)(CU)
4 A line source of strength m and a sink of strength 2m are separated a distance c.
Show that the field of flow consists in part of closed curves. Locate any stagnation points and sketch the field of flow. (U of L)
5 Derive the expression giving the stream function for irrotational flow of an
incompressible fluid past a circular cylinder of infinite span. Hence determine the position of generators on the cylinder at which the pressure is equal to that of the undisturbed stream. (Answer: ±30°, ± 150°)(U ofL)
6 Determine the stream function for a two-dimensional source of strength m. Sketch
the resultant field of flow due to three such sources, each of strength m, located at the vertices of an equilateral triangle. (U of L)
7 Derive the irrotational flow formula
P-Po = ^pU2{l — 4 sin2#)
giving the intensity of normal pressure p on the surface of a long, circular cylinder set at right-angles to a stream of velocity U. The undisturbed static pressure in the fluid is po and в is the angular distance round from the stagnation point. Describe briefly an experiment to test the accuracy of the above formula and comment on the results obtained. (U of L)
8 A long right circular cylinder of diameter am is set horizontally in a steady stream of velocity Um s-1 and caused to rotate at to rad s-1. Obtain an expression in terms of uj and U for the ratio of the pressure difference between the top and the bottom of the cylinder to the dynamic pressure of the stream. Describe briefly the behaviour of the stagnation lines of such a system as to is increased from zero, keeping V constant.
Answer. – jj~ (CU)
9 A line source is immersed in a uniform stream. Show that the resultant flow, if
irrotational, may represent the flow past a two-dimensional fairing. If a maximum thickness of the fairing is 0.15 m and the undisturbed velocity of the stream 6.0ms-1, determine the strength and location of the source. Obtain also an expression for the pressure at any point on the surface of the fairing, taking the pressure at infinity as datum. (Answer: 0.9m2 s’1, 0.0237m)(U of L)
10 A long right circular cylinder of radius am is held with its axis normal to an irrotational inviscid stream of U. Obtain an expression for the drag force acting on unit length of the cylinder due to the pressures exerted on the front half only.
^Answer: — jpU2a^j (CU)
11 Show that a velocity potential exists in a two-dimensional steady irrotational incompressible fluid motion. The stream function of a two-dimensional motion of an incompressible fluid is given by
ip^^ + bxy-^y2
where a, b and c are arbitrary constants. Show that, if the flow is irrotational, the lines of constant pressure never coincide with either the streamlines or the equipo- tential lines. Is this possible for rotational motion? (U of L)
12 State the stream function and velocity potential for each of the motions induced by a source, vortex and doublet in a two-dimensional incompressible fluid. Show that a doublet may be regarded, either as
(i) the limiting case of a source and sink, or
(ii) the limiting case of equal and opposite vortices, indicating clearly the direction of
the resultant doublet. (U of L)
13 Define (a) the stream function, (b) irrotational flow and (c) the velocity potential
for two-dimensional motion of an incompressible fluid, indicating the conditions under which they exist. Determine the stream function for a point source of strength a at the origin. Hence, or otherwise, show that for the flow due to any number of sources at points on a circle, the circle is a streamline provided that the algebraic sum of the strengths of the sources is zero. (U of L)
14 A line vortex of strength Г is mechanically fixed at the point (/, 0) referred to
a system of rectangular axes in an inviscid incompressible fluid at rest at infinity bounded by a plane wall coincident with the у-axis. Find the velocity in the fluid at the point (0, y) and determine the force that acts on the wall (per unit depth) if the pressure on the other side of the wall is the same as at infinity. Bearing in mind that this must be equal and opposite to the force acting on unit length of the vortex show that your result is consistent with the Kutta-Zhukovsky theorem. (U of L)
15 Write down the velocity potential for the two-dimensional flow about a circular
cylinder with a circulation Г in an otherwise uniform stream of velocity U. Hence show that the lift on unit span of the cylinder is pUT. Produce a brief but plausible argument that the same result should hold for the lift on a cylinder of arbitrary shape, basing your argument on consideration of the flow at large distances from the cylinder. (U of L)
16 Define the terms velocity potential, circulation, and vorticity as used in twodimensional fluid mechanics, and show how they are related. The velocity distribution in the laminar boundary layer of a wide flat plate is given by
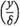 и = щ
и = щ
where uo is the velocity at the edge of the boundary layer where у equals 8. Find the vorticity on the surface of the plate.
17
A two-dimensional fluid motion is represented by a point vortex of strength Г set
at unit distance from an infinite straight boundary. Draw the streamlines and plot the velocity distribution on the boundary when Г = 7г. (U of L)
18 The velocity components of a two-dimensional inviscid incompressible flow are given by
. у. X
u = 2y————- т-рг. v = —2x————— 777
(x2+ff2 (x2 +y2)l/2
Find the stream function, and the vorticity, and sketch the streamlines.
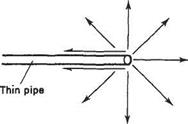
19 (a) Given that the velocity potential for a point source takes the form
Q
where in axisymmetric cylindrical coordinates (r, z)R = s/z1 + r2, show that when a uniform stream, U, is superimposed on a point source located at the origin, there is a stagnation point located on the z-axis upstream of the origin at distance
(b) Given that in axisymmetric spherical coordinates (R, ip) the stream function for the point source takes the form
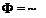 Q
Q
4-jtR
show that the streamlines passing through the stagnation point found in (a) define a body of revolution given by
2 2^(1 +cosy?)
 J ~ —
J ~ —
Make a rough sketch of this body.












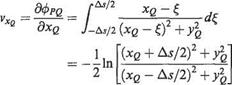
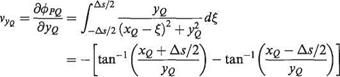 (3.97)
(3.97)

 ps = 0 and 7Г
ps = 0 and 7Г
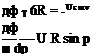 ф = — V R cos p+f (p) ф = —U R cos p + g(R)
ф = — V R cos p+f (p) ф = —U R cos p + g(R)