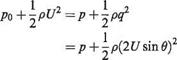The stream function due to this combination is:
■0 = sin 6 — Uy 2ttr
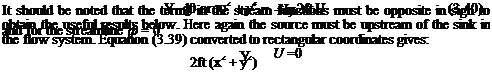
i. e.
This shows the streamline ф = 0 to consist of the Ox axis together with a circle, centre O, of radius ^/fi/(2ftU) = a (say).
Alternatively by converting Eqn (3.39) to polar coordinates:
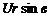 ф = J^-sind ■
ф = J^-sind ■
2ftr
Therefore
ф = sin 9 =0 for ф = 0
giving
sin в = 0 so в— 0 or ± 7Г
or
й~иг=0 ,=l^u=a
the two solutions as before.
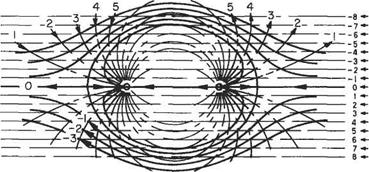
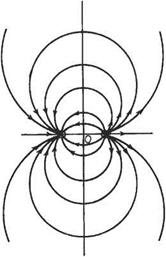
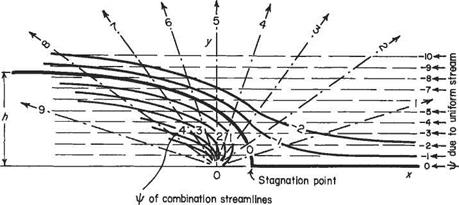
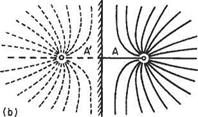
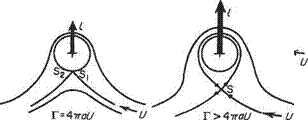
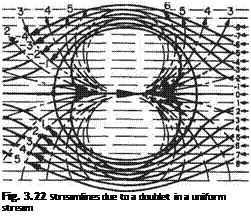
The streamline ф = 0 thus consists of a circle and a straight line on a diameter produced (Fig. 3.22). Again in this case the streamline ф = 0 separates the flow into two distinct patterns: that outside the circle coming from the undisturbed flow a long
way upstream, to flow around the circle and again to revert to uniform flow downstream. That inside the circle is from the doublet. This is confined within the circle and does not mingle with the horizontal stream at all. This inside flow pattern is usually neglected. This combination is consequently a mathematical device for giving expression to the ideal two-dimensional flow around a circular cylinder.
The velocity potential due to this combination is that corresponding to a uniform stream flowing parallel to the Ox axis, superimposed on that of a doublet at the origin. Putting x = r cos #:
li
ф = — Ur cos 0 —cos 9
 (3.41)
(3.41)
 The streamlines can be obtained directly by plotting using the superposition method outlined in previous cases. Rewriting Eqn (3.39) in polar coordinates
The streamlines can be obtained directly by plotting using the superposition method outlined in previous cases. Rewriting Eqn (3.39) in polar coordinates
Lb.
ф = -—sin# — Ur sin 9 27ГГ
and rearranging, this becomes
and with fiKlirU) = a2 a constant (a = radius of the circle^ = 0)
ф = UsmO^-rj (3.42)
Differentiating this partially with respect to r and # in turn will give expressions for the velocity everywhere, i. e.:
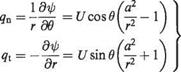 (3.43)
(3.43)
Putting r = a (the cylinder radius) in Eqns (3.43) gives:
(i) qn = Ucos#[l – 1] = 0 which is expected since the velocity must be parallel to the surface everywhere, and
(ii) qt= U sin # [1 + 1] = 2U sin #.
Therefore the velocity on the surface is 2Usin# and it is important to note that the velocity at the surface is independent of the radius of the cylinder.
The pressure distribution around a cylinder
If a long circular cylinder is set in a uniform flow the motion around it will, ideally, be given by the expression (3.42) above, and the velocity anywhere on the surface by the formula
By the use of Bernoulli’s equation, the pressure p acting on the surface of the cylinder where the velocity is q can be found. If po is the static pressure of the free stream where the velocity is U then by Bernoulli’s equation:
Therefore
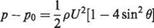 (3.45)
(3.45)
Plotting this expression gives a curve as shown on Fig. 3.23. Important points to
note are:
(1) At the stagnation points (0° and 180°) the pressure difference (p – po) is positive and equal to pU2.
(2) At 30° and 150° where sin# = A, (p — po) is zero, and at these points the local velocity is the same as that of the free stream.
(3) Between 30° and 150°CP is negative, showing that p is less than po.
(4) The pressure distribution is symmetrical about the vertical axis and therefore there is no drag force. Comparison of this ideal pressure distribution with that obtained by experiment shows that the actual pressure distribution is similar to the theoretical value up to about 70° but departs radically from it thereafter. Furthermore, it can be seen that the pressure coefficient over the rear portion of the cylinder remains negative. This destroys the symmetry about the vertical axis and produces a force in the direction of the flow (see Section 1.5.5).

|

-3.0
|
|
 |
|
|
|
ф = Ur Sin в ( – г – — 1 — — ІП – 1 1 2-k a
|
|
|
and differentiating partially with respect to r and в the velocity components of the flow anywhere on or outside the cylinder become, respectively:
|
|
|
q,-~Tr-UsM^~+’)+2„
?- = 7 % = Ucose(^-1
|
|
|
|
|
|
|
q = Jql + 4t
On the surface of the spinning cylinder r = a. Therefore,
Qn = 0
|
|
|
|
|
|
|
|
|
|
|
|
|
and applying Bernoulli’s equation between a point a long way upstream and a point on the cylinder where the static pressure is p
1 , 1 ,
Po+^PU =P + 2™
|
|
|
|
|
|
|
|
|
|
|
|
This equation differs from that of the non-spinning cylinder in a uniform stream of the previous section by the addition of the term (Tj(2-KUa)) = В (a constant), in the squared bracket. This has the effect of altering the symmetry of the pressure distribution about a horizontal axis. This is indicated by considering the extreme top and bottom of the cylinder and denoting the pressures there by pj and рв respectively. At the top p =pr when 9 = тг/2 and sin в = 1. Then Eqn (3.49) becomes
PT-po=pU2{-[2 + B2)

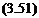 = – X-pU2(3 + 4B + Bz)
= – X-pU2(3 + 4B + Bz)
At the bottom p — Pb when 9 = – тг/2 and sin 9 = -1:
Pb-Po = -pU2{3-4B + B2)
Clearly (3.50) does not equal (3.51) which shows that a pressure difference exists between the top and bottom of the cylinder equal in magnitude to
which suggests that if the pressure distribution is integrated round the cylinder then a resultant force would be found normal to the direction of motion.
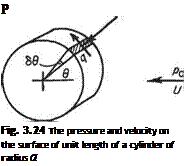
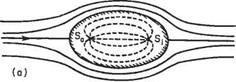
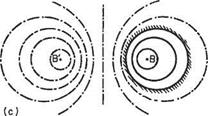
The normal force on a spinning circular cylinder in a uniform stream
Consider a surface element of cylinder of unit span and radius a (Fig. 3.24). The area of the element = а 89 x 1, the static pressure acting on element = p, resultant force = ip— po)a69, vertical component = ip— po)a69 sin9.
Substituting for ip — po) from Eqn (3.49) and retaining the notation В = rj2irUa, the vertical component of force acting on the element = pU2[ 1 — (2 sin 9 + Bf]a 69 sin 9. The total vertical force per unit span by integration is (/ positive upwards):
which becomes
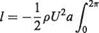
[sin 9( 1 – B2) – 4В sin2 9 — 4 sin3 9]й9
On integrating from 0 to 2тг the first and third terms vanish leaving
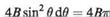
r2 r
Replacing В by Гj2irUa and cancelling gives the equation for the lift force per unit span
l 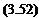 = pUT
= pUT
The lift per unit span in N is equal to the product of density p, the linear velocity U, and the circulation Г.
This expression is the algebraic form of the Kutta-Zhukovsky theorem, and is valid for any system that produces a circulation superimposed on a linear velocity (see Section 4.1.3). The spinning cylinder is used here as it lends itself to stream function theory as well as being of interest later.
It is important to note that the diameter of the cylinder has no influence on the final expression, so if a line vortex of strength Г moved with velocity U in a uniform flow of density p, the same sideways force / = pUT per unit length of vortex would be found. This sideways force commonly associated with a spinning object moving through the air has been recognized and used in ball games since ancient times. It is usually referred to as the Magnus effect after the scholar and philosopher Magnus.
![]() (3.53)
(3.53)![]() = pr8r66q^/r
= pr8r66q^/r![]() dp _ pgj
dp _ pgj![]() dH = d{p + pq) = dr dr
dH = d{p + pq) = dr dr![]() (3.56)
(3.56)










 The streamlines can be obtained directly by plotting using the superposition method outlined in previous cases. Rewriting Eqn (3.39) in polar coordinates
The streamlines can be obtained directly by plotting using the superposition method outlined in previous cases. Rewriting Eqn (3.39) in polar coordinates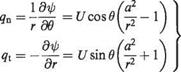 (3.43)
(3.43)