In discussing aerodynamic force it is necessary to know how the dependent variables, aerodynamic force and moment, vary with the independent variables thought to be relevant.
Assume, then, that the aerodynamic force, or one of its components, is denoted by F and when fully immersed depends on the following quantities: fluid density p, fluid kinematic viscosity v, stream speed V, and fluid bulk elasticity K. The force and moment will also depend on the shape and size of the body, and its orientation to the stream. If, however, attention is confined to geometrically similar bodies, e. g. spheres, or models of a given aeroplane to different scales, the effects of shape as such will be eliminated, and the size of the body can be represented by a single typical dimension; e. g. the sphere diameter, or the wing span of the model aeroplane, denoted by D. Then, following the method above
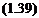 F = f(F, D, p, v, K) = EC Vа Dbpcifl Ke
F = f(F, D, p, v, K) = EC Vа Dbpcifl Ke
In dimensional form this becomes
Equating indices of mass, length and time separately leads to the three equations:
With five unknowns and three equations it is impossible to determine completely all unknowns, and two must be left undetermined. These will be d and e. The variables whose indices are solved here represent the most important characteristic of the body (the diameter), the most important characteristic of the fluid (the density), and the speed. These variables are known as repeated variables because they appear in each dimensionless group formed.
The Eqns (1.40) may then be solved for a, b and c in terms of d and e giving
a — 2 — d — 2e
b = 2-d
c = 1-е
Substituting these in Eqn (1.39) gives
F = V2~d~2eD1~dp[~ei/Ke
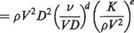 (1.41)
(1.41)
The speed of sound is given by Eqns (1.6b, d) namely,
p p
Then
 p V2 pV2
p V2 pV2
and Via is the Mach number, M, of the free stream. Therefore Eqn (1.41) may be written as
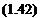 F = pV2D2g(^]h{M)
F = pV2D2g(^]h{M)
where g(VD/v) and h(M) are undetermined functions of the stated compound variables. Thus it can be concluded that the aerodynamic forces acting on a family of geometrically similar bodies (the similarity including the orientation to the stream), obey the law
This relationship is sometimes known as Rayleigh’s equation.
The term VDjv may also be written, from the definition of v, as pVD/p, as above in the problem relating to the eddy frequency in the flow behind a circular cylinder. It is a very important parameter in fluid flows, and is called the Reynolds number.
Now consider any parameter representing the geometry of the flow round the bodies at any point relative to the bodies. If this parameter is expressed in a suitable non-dimensional form, it can easily be shown by dimensional analysis that this non-dimensional parameter is a function of the Reynolds number and the Mach number only. If, therefore, the values of Re (a common symbol for Reynolds number) and M are the same for a number of flows round geometrically similar bodies, it follows that all the flows are geometrically similar in all respects, differing only in geometric scale and/or speed. This is true even though some of the fluids may be gaseous and the others liquid. Flows that obey these conditions are said to be dynamically similar, and the concept of dynamic similarity is essential in wind-tunnel experiments.
It has been found, for most flows of aeronautical interest, that the effects of compressibility can be disregarded for Mach numbers less than 0.3 to 0.5, and in cases where this limit is not exceeded, Reynolds number may be used as the only criterion of dynamic similarity.
|
Example 1.1 An aircraft and some scale models of it are tested under various conditions, given below. Which cases are dynamically similar to the aircraft in flight, given as case (А)?
|
Case (A)
|
Case (B)
|
Case (C)
|
Case (D)
|
Case (E)
|
Case (F)
|
|
Span (m)
|
15
|
3
|
3
|
1.5
|
1.5
|
3
|
|
Relative density
|
0.533
|
1
|
3
|
1
|
10
|
10
|
|
Temperature (°С)
|
-24.6
|
+ 15
|
+15
|
+ 15
|
+15
|
+15
|
|
Speed (TAS) (ms-1)
|
100
|
100
|
100
|
75
|
54
|
54
|
Case (A) represents the full-size aircraft at 6000 m. The other cases represent models under test in various types of wind-tunnel. Cases (С), (E) and (F), where the relative density is greater than unity, represent a special type of tunnel, the compressed-air tunnel, which may be operated at static pressures in excess of atmospheric.
|
From the figures given above, the Reynolds number VDpjp, may be calculated for each case. These are found to be
It is seen that the values of Re for cases (C) and (E) are very close to that for the full-size aircraft. Cases (A), (C) and (E) are therefore dynamically similar, and the flow patterns in these three cases will be geometrically similar. In addition, the ratios of the local velocity to the free stream velocity at any point on the three bodies will be the same for these three cases. Hence, from Bernoulli’s equation, the pressure coefficients will similarly be the same in these three cases, and thus the forces on the bodies will be simply and directly related. Cases (B) and (D) have Reynolds numbers considerably less than (A), and are, therefore, said to represent a ‘smaller aerodynamic scale’. The flows around these models, and the forces acting on them, will not be simply or directly related to the force or flow pattern on the full-size aircraft. In case (F) the value of Re is larger than that of any other case, and it has the largest aerodynamic scale of the six.
Example 1.2 An aeroplane approaches to land at a speed of 40m s-1 at sea level. A l/5th scale model is tested under dynamically similar conditions in a Compressed Air Tunnel (CAT) working at 10 atmospheres pressure and 15 °С. It is found that the load on the tailplane is subject to impulsive fluctuations at a frequency of 20 cycles per second, owing to eddies being shed from the wing-fuselage junction. If the natural frequency of flexural vibration of the tailplane is 8.5 cycles per second, could this represent a dangerous condition?
For dynamic similarity, the Reynolds numbers must be equal. Since the temperature of the atmosphere equals that in the tunnel, 15 °С, the value of p. is the same in both model and full-scale cases. Thus, for similarity
Vf£?fPf — Vmdmpm
In this case, then, since
giving
Vm = 20 ms-1
Now Eqn (1.38) covers this case of eddy shedding, and is
For dynamic similarity
Therefore
«r x 1 20 x I
40 = 20
This is very close to the given natural frequency of the tailplane, and there is thus a considerable danger that the eddies might excite sympathetic vibration of the tailplane, possibly leading to structural failure of that component. Thus the shedding of eddies at this frequency is very dangerous to the aircraft.
Example 1.3 An aircraft flies at a Mach number of 0.85 at 18300m where the pressure is 7160Nm-2 and the temperature is —56.5 °С. A model of l/10th scale is to be tested in a highspeed wind-tunnel. Calculate the total pressure of the tunnel stream necessary to give dynamic similarity, if the total temperature is 50 °С. It may be assumed that the dynamic viscosity is related to the temperature as follows:
where Tb = 273 °С and po = 1.71×10 5kgm [s 1 (i) Full-scale aircraft

M = 0.85, a = 20.05(273 – 56.5)I/2 = 297ms-1
V = 0.85 x 297 = 252 ms-1
p = x 10 5 = 1.44 x 10 5 kgm 1 s 1
Consider a dimension that, on the aircraft, has a length of 10 m. Then, basing the Reynolds number on this dimension:

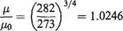
n = 1.71 x 1.0246 x КГ5 = 1.751 x lO^kgnT1 s_1
For dynamic similarity the Reynolds numbers must be equal, i. e.
giving
p = 1.23 kg m 3
Thus the static pressure required in the test section is
p = pRT = 1.23 x 287.3 x 282 = 99 500NnT2 The total pressure p% is given by
(l+±M2) = (1.1445)35 = 1.605
ps = 99 500 x 1.605 = 160000NitT2
If the total pressure available in the tunnel is less than this value, it is not possible to achieve equality of both the Mach and Reynolds numbers. Either the Mach number may be achieved at a lower value of Re or, alternatively, Re may be made equal at a lower Mach number. In such a case it is normally preferable to make the Mach number correct since, provided the Reynolds number in the tunnel is not too low, the effects of compressibility are more important than the effects of aerodynamic scale at Mach numbers of this order. Moreover, techniques are available which can alleviate the errors due to unequal aerodynamic scales.
In particular, the position at which laminar-turbulent transition (see Section 7.9) of the boundary layer occurs at full scale can be fixed on the model by roughening the model surface. This can be done by gluing on a line of carborundum powder.












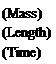
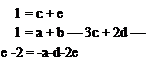

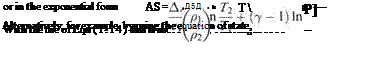
 -t
-t